Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 2.Problemas - Ex. 25
Uma barra cilíndrica de aço inoxidável encontra-se isolada em sua lateral e não nas extremidades. A distribuição de temperaturas em regime estacionário é , em que e . O diâmetro e o comprimento da barra são e , respectivamente. Determine o fluxo térmico ao longo da barra . Sugestão: A massa da barra é .
Passo 1
Nessa questão, nós temos o diâmetro, comprimento e massa de uma barra de aço inoxidável isolada em sua superfície externa, exceto nas extremidades. Além disso, temos também a distribuição de temperatura. Ilustrando isso, temos:
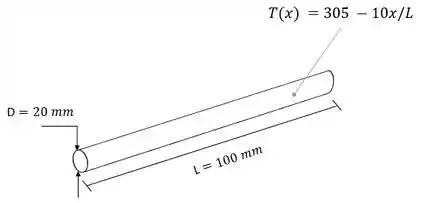
Essas informações são para que possamos calcular o fluxo de calor, beleza? Então vamos lá!
Passo 2
Para resolver essa questão, vamos assumir que estamos em condição de estado estacionário, (a condução é unidimensional na direção x e as propriedades são constantes.
A partir da Lei de Fourier para o fluxo de calor, temos:
A Tabela A.1 fornece valores para a condutividade térmica dos aços inoxidáveis, no entanto, não nos dizem de que tipo de aço inoxidável a haste é feita mas sabemos que a condutividade térmica varia entre eles.
Então, conhecendo a massa da barra e podemos usá-la para calcular sua densidade:
Passo 3
Na Tabela A.1, vemos que o material é de aço inoxidável AISI 304. A temperatura da barra varia de a . Avaliando a condutividade térmica a , .Então,