Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 7.Exercício - Ex. 6

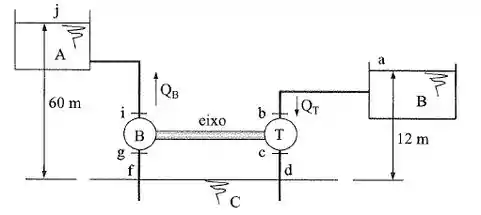
Numa certa região, há três reservatórios naturais, A, B e C, e um conjunto TB formado por uma turbina acoplada diretamente a uma bomba. As perdas de carga nas tubulações são:

Entre a e b, H p a , b = 0,5   m

Entre c e d, H p c , d = 0,4   m

Entre f e g, H p f , g = 0,6   m

Entre i e j, H p i , j = 0,4   m

E o rendimento do conjunto TB, η T B = η T × η B = 0,6 . Sendo T = turbina e B = bomba, determinar a relação entre as vazões Q T e Q B na turbina e na bomba, respectivamente.

Fluido: água de γ = 10 4   N / m 3 .

Passo 1

Vamos começar esse exercício encontrando a carga da turbina, para isso vamos aplicar o equilíbrio de energia entre os pontos a e d:

H a - H T = H d + H p a , d

v a 2 2 g + p a γ + z a - H T = v d 2 2 g + p d γ + z d + H p a , d

Substituindo os valores conhecidos:

0 2 2 g + 0 γ + 12 - H T = 0 2 2 g + 0 γ + 0 + H p a , b + H p c , d

H T = 12 - 0,5 - 0,4 → H T = 11,1   m

Passo 2

Agora vamos calcular a carga da bomba aplicando o equilíbrio de energia entre os pontos f e j:

H f + H B = H j + H p f , j

v f 2 2 g + p f γ + z f + H B = v j 2 2 g + p j γ + z j + H p f , j

Substituindo os valores conhecidos:

0 2 2 g + 0 γ + 0 + H B = 0 2 2 g + 0 γ + 6 0 + H p f , g + H p i , j

H B = 6 0 + 0,6 + 0,4 → H B = 6 1   m

Passo 3

Nesse exercício, como a turbina e a bomba estão acopladas ao mesmo eixo, então elas compartilham a mesma potência, dessa forma, igualando suas potências, temos:

N B = N T → γ Q B H B η B = η T γ Q T H T → Q T Q B = H B η B η T H T

Substituindo os valores conhecidos e o valor de η B × η T dado no enunciado, temos:

Q T Q B = 61 0,6 ( 11,1 ) → Q T Q B = 9,16

Resposta

Q T Q B = 9,16

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na instalação da figura, determinar:a) a altura h ;b) o tipo de máquina;c) a potência da máquina se η M = 70 % Dados: Q = 31,4L / s ; tg ⁡ β = 0,2 ; γ = 8000N / m 3 ; ν = 10 - 4m 2 / s ; k s 1 = 16 ;
Considere um escoamento incompressível em um duto circular. Deduza expressões gerais para o número de Reynolds em termos de (a) vazão volumétrica e diâmetro do tubo (b) vazão mássica e diâmetro do tub
Ar a 100°C entra em um duto circular de diâmetro 125 mm. Encontre a vazão volumétrica na qual o escoamento torna-se turbulento. Para essa vazão, estime o comprimento de entrada necessário para estabel
Considere o escoamento do tubo da torre de água do Exemplo 8.7. Após 5 anos, a rugosidade do tubo aumentou de modo que o escoamento tornou-se completamente turbulento e f=0,04 . Determine de quanto a
A velocidade média de escoamento em um trecho de diâmetro constante da tubulação do Alasca é 2,5 m/s. Na entrada, a pressão é 8,25 MPa (manométrica) e a elevação é 45 m; na saída, a pressão é 350 kPa