Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 7.Exercício - Ex. 7
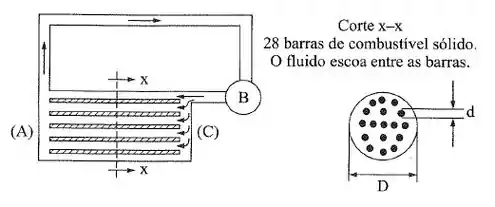
Entre A e C do circuito hidráulico da figura está um conjunto de elementos combustíveis usado em reatores nucleares. Desprezam-se as perdas no resto do circuito e são dados: ; ; ; .
Calcular a rugosidade equivalente dos materiais de que são feitos os tubos externos e internos.
Passo 1
Nesse exercício, como o enunciado nos disse que a perda de carga no resto do circuito devem ser desprezadas, então a carga fornecida pela bomba deve ser igual a perda de carga entre A e C, então:
Com isso, podemos encontrar a vazão no sistema através da fórmula de potência da bomba:
Substituindo os valores conhecidos:
Então, agora podemos encontrar a velocidade do fluido na tubulação através da fórmula da vazão:
Só que nesse exercício temos as 28 barras de combustível sólido dentro da tubulação por onde escoa o fluido, então a área útil da tubulação será a área total do tubo menos a área dessas 28 barras, então, temos:
Substituindo os valores conhecidos:
Agora, voltando para a fórmula da vazão:
Passo 2
Agora, sabemos que a perda de carga distribuída é dada por:
No nosso caso, como não temos uma seção uniforme, precisamos encontrar o valor do diâmetro hidráulico, então, lembrando da equação 7.3 apresentada nessa seção do livro:
E, agora da equação 7.2:
Então, teremos:
No caso, essa área é a área útil da seção, que já calculamos no passo 1, agora precisamos encontrar o valor de que é o perímetro molhado, como o nome já diz, é toda superfície que está em contato com o líquido, então seria a circunferência externa maior da tubulação mais as 28 circunferências dos tubos menores, então temos:
Então, substituindo esse valor na equação para , temos:
Passo 3
Agora vamos retornar à equação da perda de carga distribuída mostrada no passo 2 e isolar o fator de atrito :
E, substituindo os valores conhecidos:
Agora vamos encontrar o número de Reynolds para esse escoamento:
Passo 4
Agora vamos olhar o diagrama de Moody a seguir para encontrar a curva que contém e :
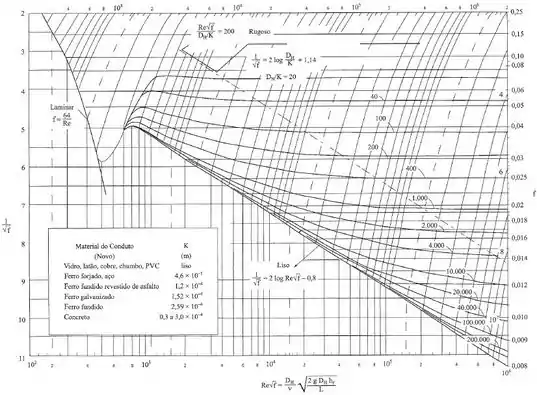
Através do diagrama, podemos ver que a curva que intercepta esses pontos está um pouco abaixo daquela , então, podemos adotar (para o valor ficar coerente com o gabarito):