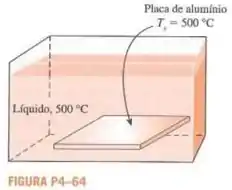
Uma chapa de alumínio de espessura de é aquecida em líquido com temperatura de . A placa de alumínio tem temperatura uniforme inicial de . Considerando que a temperatura da superfície da placa de alumínio é aproximadamente a temperatura do líquido, determine a temperatura no centro da placa após segundos de aquecimento.

Como a temperatura da superfície da placa é igual à temperatura do líquido, o coeficiente de transferência de calor por convecção é infinitivo.

Assim, podemos calcular o número do Biot usando a seguinte relação:

Aqui  é o comprimento característico e  é a condutividade térmica do material da placa. Substituindo os termos da equação pelos valores conhecidos, temos:

Podemos obter as constantes e para a placa na tabela 4-2, correspondentes ao número Biot encontrado acima para parede plana. Assim, temos que:

Agora, vamos calcular o número de Fourier usando a seguinte relação:

Aqui  é o número de Fourier, é a difusividade térmica,  é o tempo e é o comprimento crítico da placa. Substituindo os termos da equação pelos dados conhecido, temos:

Como o número de Fourier é maior que , o método de aproximação de um termo é usado para resolver o problema.

Vamos calcular a temperatura no plano central da placa de alumínio usando a seguinte relação:

Podemos reescrever ainda a equação da seguinte maneira:

Aqui  é a temperatura do plano central,  é a temperatura do fluido e  é a temperatura inicial da placa. Substituindo os termos pelos dados conhecido, temos:

Portanto, a temperatura do plano central da placa de alumínio após 15 segundos de aquecimento é .