Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 75

Um coeficiente de quantidade de movimento, β , é definido como:

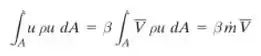
Avalie β para um perfil de velocidade laminar, Eq. 8.14, e para um perfil de velocidade turbulenta de “lei de potência”, Eq. 8.22. Trace β como uma função de n para perfil turbulento de lei de potência na faixa 6   ≤   n   ≤   10 e compare com o caso do escoamento laminar completamente desenvolvido em tubo.

Passo 1

Fala aí galera, vamos para mais um problema de Mecânica dos fluidos. Primeiramente, sabemos que, para o escoamento laminar:

β = 1 m ˙ V - ∫ u ρ u d A = 1 ρ V - π R 2 V -   ∫ 0 R u ρ u 2 π r d r  

Como u U = f r R :

β = 1 ρ π R 2   U V - 2 ∫ 0 R u U 2 2 ρ π r d r = 2 U V - ² ∫ 0 1 u U 2 r R d r R  

Como o escoamento é laminar:

u U = 1 - r R 2

Logo:

u U 2 = 1 - 2 r R 2 + r R 4

Portanto:

β = 2 U V - 2 ∫ 0 1 r R - 2 r R 3 + r R 5 d r R = 2 U V - 2 1 2 - 1 2 + 1 6

Por fim, como U = 2 V - :

β = 1 3 2 2 = 4 3

Passo 2

Agora, para um escoamento turbulento, temos que:

u U = 1 - r R 1 n

u U 2 = 1 - r R 2 n

Logo:

β = 2 U V - 2 ∫ 1 0 1 - r R 2 n r R d r R

Se fizermos a substituição:

m = 1 - r R

r R = 1 - m

d r R = - d m

Substituindo e resolvendo a integral (nosso foco aqui não é resolver integrais, para isso, temos os módulos de cálculo, qualquer dúvida, só olhar lá):

β = 2 U V - 2 n 2 n + 2 2 n + 2

Como 1 = 7 :

β = 1 0,817 2 2 × 7 2 9 × 16 = 0,817

Passo 3

Para plotar o gráfico β × n :

V - U = 2 n 2 n + 1 2 n + 1

β = U V - 2 n 2 n + 2 n + 1

Portanto:

β = n + 1 2 n + 1 2 4 n 2 n + 2

Plotando o gráfico:

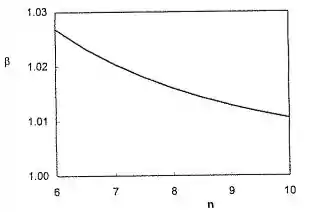
Resposta

β = 4 3

β = 0,817

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um escoamento completamente desenvolvido em um tubo cilíndrico de raio R e comprimento L = 10m m , com o escoamento gerado pela aplicação de um gradiente de pressão Δ p . Testes foram realiz
O experimento “pitchdrop” (piche em queda) vem sendo repetido continuamente na Universidade de Queensland desde 1927 (http://www.physics.uq.edu.au/physics_museum/pitchdrop.shtml). Neste experimento, u
No esquema da figura, o nível da água é mantido constante. Determinar:O coeficiente de velocidade;O número de Reynolds teórico;O tempo que a água levará para subir 10c m ao fechar o registro do bocal;
Num trecho de conduto retangular 20c m × 40c m para ventilação, escoa ar ( ρ = 1,2k g / m 3 ) , considerado incompressível, com uma vazão de 2m 3 / s . Determinar:O coeficiente de perda de carga singu
Uma sala de 4m × 6m × 3m é usada como cabine de pintura. Sabe-se que numa cabine de pintura o ar ( ρ = 1,2k g / m 3( c o n s t a n t e ) ; v = 10 - 5m 2 / s ) deve ser trocado, por norma, no mínimo 60