Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 58

Considere um escoamento completamente desenvolvido em um tubo cilíndrico de raio R e comprimento L = 10   m m , com o escoamento gerado pela aplicação de um gradiente de pressão Δ p . Testes foram realizados com água a temperatura ambiente para vários valores de R , com uma vazão fixada Q = 10   μ L / m i n . A resistência hidráulica é definida por R h i d = Δ p / Q em analogia com a resistência elétrica R e l é t = Δ V / I , em que Δ V é a queda de potencial elétrico e I é a corrente elétrica). Calcule o gradiente de pressão requerido e a resistência para os raios de tubo listados na tabela. Baseado no resultado, você acha que seria apropriado usar um gradiente de pressão para bombear fluidos em microcanais, ou deveria ser usado algum outro tipo de mecanismo de impulsão?

Passo 1

Neste problema é necessário calcular a resistência hidráulica ( R h i d ), a qual é definida como função do gradiente de pressão e da vazão:

R h i d = ∆ p Q

Por se tratar de um escoamento completamente desenvolvido ao longo de um tubo circular, a vazão é denida por:

Q = π ∆ p R 4 8 μ L

Com as informações características do escoamento e tubulação fornecidas no enunciado ( L   = 10 mm e Q =10 μ L/min) é possível calcular a queda de pressão ( ∆ p ) e com tal resultado a resistência hidráulica.

Passo 2

A fim de obter o gradiente de pressão, a expressão da vazão deve ser arranjada da seguinte forma:

Q = π ∆ p R 4 8 μ L

∆ p = 8 μ L Q π R 4

Passo 3

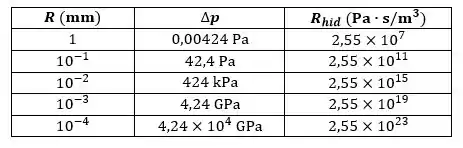
A partir dos dados do problema o gradiente de pressão pode ser calculado (atenção, as grandezas devem estar em metro e segundo) para os diferentes valores de R do tubo:

∆ p = 8 ( 1 × 10 - 3 ) ( 10 × 10 - 3 ) ( 10 × 10 - 6 × 10 - 3 60   ) π R 4

- para R = 1 mm

∆ p = 0,00424   P a

- para R = 10 - 1 mm

∆ p = 42,4   P a

- para R = 10 - 2 mm

∆ p = 424   k P a

- para R = 10 - 3 mm

∆ p = 4,24   G P a

- para R = 10 - 4 mm

∆ p = 4,24 × 10 4   G P a

Passo 4

Já a resistência hidráulica é obtida pela relação:

R h i d = ∆ p Q

R h i d = 8 μ L Q π R 4 Q

R h i d = 8 μ L π R 4

Considerando os dados numéricos do problema, a resistência hidráulica pode ser calculada para os diferentes valores de R do tubo, conforme:

R h i d = 8 ( 1 × 10 - 3 ) ( 10 × 10 - 3 ) π R 4

- para R = 1 mm

R h i d = 2,55 × 10 7   P a ∙ s / m 3

- para R = 10 - 1 mm

R h i d = 2,55 × 10 11   P a ∙ s / m 3

- para R = 10 - 2 mm

R h i d = 2,55 × 10 15   P a ∙ s / m 3

- para R = 10 - 3 mm

R h i d = 2,55 × 10 19   P a ∙ s / m 3

- para R = 10 - 4 mm

R h i d = 2,55 × 10 23   P a ∙ s / m 3

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tubo que transporta óleo a 40 ° C a uma taxa de 3 m 3 s , se divide em dois tubos paralelos feitos de aço comercial que se reconectam a jusante. O tubo A tem 500m de comprimento e diâmetro de 30c m
Um tubo circular de água tem uma expansão abrupta do diâmetro D 1 = 15c m para D 2 = 20c m . A pressão e a velocidade média da água no tubo menor são P 1 = 120k P a e 10m / s , respectivamente, e o es
Em uma usina hidrelétrica a água a 20 ° C é fornecida para a turbina a uma taxa de 0,8m 3 / s através de um tubo de ferro fundido com 200m de comprimento e 0,35m de diâmetro. A diferença de elevação e
No Problema 8 - 112 , o diâmetro do tubo é triplicado para reduzir as perdas do tubo. Determine o aumento percentual na saída de potência liquida como resultado dessa modificação.
A água em uma piscina acima do solo a 20 ° C , com 10m de diâmetro e 2m de altura deve ser esvaziada destampando um tubo plástico horizontal com 3c m de diâmetro e 25m de comprimento anexado à parte i