Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 79

Um coletor solar é formado por um longo duto através do qual ar é soprado; sua seção transversal forma um triângulo equilátero com 1 m de lado. Um dos lados é uma cobertura de vidro com emissividade ε1 = 0,9, enquanto os outros dois lados são placas de absorção com ε2 = ε3 = 1,0.

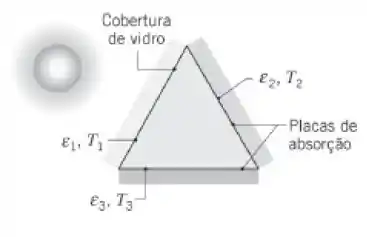
Durante a operação, sabe-se que as temperaturas superficiais são T1 =25°C, T2 = 60°C e T3 = 70°C. Qual é a taxa líquida na qual a radiação é transferida para a cobertura devido à troca com as placas de absorção?

Passo 1

Vamos lá!! Queremos saber qual é a taxa líquida de radiação q 1 que chega na cobertura! Para isso temos:

q 1 = E b 1 - J 1 1 - ε 1 ε 1 A 1

O problema é que não conhecemos J 1 , então precisamos de uma outra expressão!! Para isso vamos usar a expressão 13.21 :

E b - J 1 1 - ε 1 ε 1 A 1 = ∑ j = 1 N J 1 - J j A i F i j - 1

Temos duas superfícies trocando calor com a superfície 1 , então:

E b 1 - J 1 = 1 - ε 1 ε 1 F 12 J 1 - J 2 + F 13 J 1 - J 3

Passo 2

Os fatores de forma a gente pode encontrar usando algumas propriedades!!

Pela regra da soma:

F 12 + F 13 = 1

Pela simetria:

F 12 = F 13

Logo:

F 12 = F 13 = 0,5

Lembrando que ε 2 = ε 3 = 1 , logo são superfícies negras, então J 2 = E b 2 e J 3 = E b 3 :

E b 1 - J 1 = 1 - 0 , 9 0,9 0,5 J 1 - E b 2 + 0,5 J 1 - E b 3

Isolando J 1 :

J 1 = E b 1 + 0,556 ( E b 2 + E b 3 ) 1,111

Substituindo:

J 1 = 5,67 × 10 - 8 × 298 4 + 0,556 5,67 × 10 - 8 × 333 4 + ( 5,67 × 10 - 8 × 343 4 ) 1,111

Calculando:

J 1 = 478,64   W / m 2

Passo 3

Agora vamos voltar pra cá:

q 1 = E b 1 - J 1 1 - ε 1 ε 1 A 1

Substituindo:

q 1 = 5,67 × 10 - 8 × 298 4 - 478,64 1 - 0,9 0,9 × 1 l

Calculando:

q 1 = - 265,5   l   W

Ou, se quisermos a taxa por unidade de comprimento:

q 1 ' = - 265,5   W / m

Resposta

q 1 ' = - 265,5   W / m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um gabinete composto por 13 superfícies. Quantos fatores de forma tem essa geometria? Quantos desses fatores de forma podem ser determinados pela aplicação das regras de reciprocidade e da a
Duas placas paralelas infinitamente longas de largura w são separadas por uma distância w, como mostrado abaixo. Usando o método de linhas cruzadas de Hottel, determine o fator de forma F12.
Como você pode determinar o fator de forma F 12 quando o fator de forma F 21 e as áreas das superfícies estão disponíveis?
Considere um invólucro cilindro com A1, A2 e A3, representando as bases interas e superior e as superfícies lateriais, respectivamente. Usando a razão de comprimento de diâmetro K = L/D, determina (a)
Considere uma pessoa cuja superfície exposta é de 1,9m 2 com emissividade de 0,85 e temperatura da superfície de 30 ° C . Determine a taxa de perda de calor por radiação dessa pessoa para uma grande s