Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 81

A vigia cilíndrica em uma parede de fornalha com espessura L = 250 mm tem um diâmetro D = 125 mm. O interior da fornalha está a uma temperatura de 1300 K e a vizinhança externa à fornalha tem uma temperatura de 300 K.

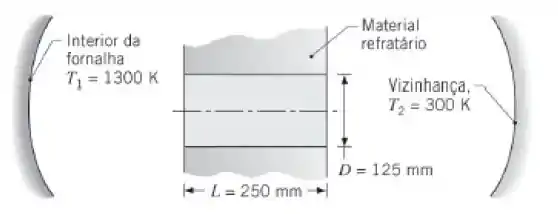
Determine a perda térmica por radiação através da vigia.

Passo 1

Vamos lá!! Essa vigia cilíndrica na parede da fornalha é nada mais nada menos do que um buraco no formato de um cilindro de 125   m m de diâmetro, por isso a perda de calor!!

Nesse esqueminha do livro o que vc ta olhando é um buraco na forma de um cilindro deitado, beleza?!

Vamos ver um esqueminha simplificado:

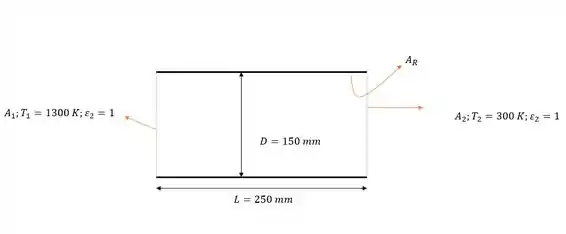
As superfícies 1 e 2 são superfícies abertas, então elas tem emissividade ε 1 = ε 2 = 1 e o calor que sai da superfície 1 é igual ao que chega na superfície 2 que é igual a perda!!

Temos um sistema simétrico e a superfície R é isolada, dessa forma:

q p e r d a = q 1 = - q 2 = σ ( T 1 4 - T 2 4 ) 1 - ε 1 ε 1 A 1 + 1 A 1 F 12 + 1 A 1 F 1 R + 1 A 2 F 2 R - 1 + 1 - ε 2 ε 2 A 2

Como A 1 = A 2 e ε 1 = ε 2 = 1 , simplificamos:

q 1 = A σ ( T 1 4 - T 2 4 ) 1 F 12 + 1 F 1 R + 1 F 2 R - 1

Passo 2

Lembra que a gente tem um cilindro deitado?!! Então temos discos paralelos coaxiais, para descobrir F 1 2 , vamos usar as relações da tabela 13.2 :

R 1 = R 2 = r L = 125 2 250 = 0,25

S = 1 + 1 + R 2 2 R 1 2 = 1 + 1 + 0,25 2 0,25 2 = 18

Para calculr F 12 :

F 1 2 = 1 2 S - S 2 - 4 D 2 D 1 2 1 2

Substituindo:

F 1 2 = 1 2 18 - 18 2 - 4 125 125 2 1 2 = 0 , 05573

Pela regra da soma:

F 1 R = 1 - 0,05573 = 0 , 9443

Por simetria:

F 1 R = F 2 R

Passo 3

Agora podemos substituir:

q 1 = π × 0,125 4 4 × 5,67 × 10 - 8 ( 1300 4 - 300 4 ) 1 0,05573 + 1 0,9443 + 1 0,9443 - 1

Calculando:

q 1 = q p e r d i d o = 1046   W

Resposta

q p e r d i d o = 1046   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um novo equipamento de reciclagem por infravermelho foi proposto para reciclar os milhões de quilos de plásticos descartados pelo desmonte e prensagem de veículos automotivos após sua “aposentadoria”.
35 – Duas grandes placas paralelas são mantidas a T1 = 500 K e T2 = 300 K, respectivamente. A placa quente tem uma emissividade de 0,9 enquanto que a placa fria tem emissividade de 0,7.A) Determine o
32 – A eq. 1.7 é subjetiva a diversas restrições, tal como a vizinhança sendo isotérmica e grande em relação a superfície menores. Considere uma superfície pequena e grande de esferas concêntricas de
48 – Um longo condute é construído com paredes amplas cinzas e difusivas de 0,5 m. O topo e o fundo do condute está isolado. As emissividades das paredes são ε1 = 0,45, ε2 = 0,65 e ε3 = 0,15, respecti
2 – Uma partícula esférica de raio r1= 5 mm está suspensa por um fio fino dentro de um tubo cilíndrico de raio interno r2 = 15 mm e comprimento L = 0,5 m. Determine os fatores de forma F11, F12, F13 e