Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 75

Considere um longo duto construído com paredes cinzas e difusas, com 1 m de lado.

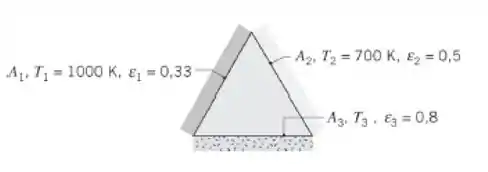
  1. Determine a transferência de radiação líquida saindo da superfície A 1 por unidade de comprimento do duto.

  2. Determine a temperatura da superfície com isolamento térmico A 3 .

  3. Qual seria o efeito de variar ε 3 no seu resultado? Após analisar as suas hipóteses, comente se você espera que os seus resultados sejam exatos.

Passo 1

Vamos lá!!

Começando pela letra a ! O enunciado é bem direto, queremos q 1 ' , como a superfície 3 esta isolada, então usamos a seguinte expressão:

q 1 = σ ( T 1 4 - T 2 4 ) 1 - ε 1 ε 1 A 1 + 1 A 1 F 12 + 1 A 1 F 1 3 + 1 A 2 F 2 3 - 1 + 1 - ε 2 ε 2 A 2

Se:

q 1 ' = q 1 l

Então:

q ' 1 = σ ( T 1 4 - T 2 4 ) 1 - ε 1 ε 1 A ' 1 + 1 A ' 1 F 12 + 1 A ' 1 F 1 3 + 1 A ' 2 F 2 3 - 1 + 1 - ε 2 ε 2 A ' 2

Como todos os lados são iguais A 1 ' = A 2 ' = A 3 ' = 1

q ' 1 = σ ( T 1 4 - T 2 4 ) 1 - ε 1 ε 1 + 1 F 12 + 1 F 13 + 1 F 23 - 1 + 1 - ε 2 ε 2

Passo 2

Precisamos conhecer os fatores de forma!!

Por simetria:

F 31 = F 32

Pela regra da soma:

F 31 + F 32 = 1

Logo:

F 31 = F 32 = 0,5  

Como A 1 ' = A 3 '

F 13 = F 31 = 0,5

Pela regra da soma:

F 23 = 1 - 0,5 = 0,5

Passo 3

Podemos achar q 1 ' , lembrando que σ = 5,67 × 10 - 8 W / m 2 K 4 :

q ' 1 = 5,67 × 10 - 8 ( 1000 4 - 700 4 ) 1 - 0,33 0,33 + 1 0,5 + 1 0,5 + 1 0,5 - 1 + 1 - 0,5 0,5

Calculando:

q 1 ' = 9874   W / m

Passo 4

Agora queremos saber a temperatura da superfície isolada, T 3 !! Vamos fazer um balanço da radiação:

q R = q 3 = 0 = E b 3 - J 1 1 A 3 F 31 + E b 3 - J 2 1 A 2 F 3 2

Como A 3 = A 2 e F 31 = F 32 :

E b 3 = J 1 + J 2 2

Sabendo que :

E b 3 = σ T 3 4

E daqui que vai sair a temperatura!!!

Substituindo e isolando T 3 :

T 3 = J 1 + J 2 2 σ 1 4

Passo 5

Mas primeiro precisamos conhecer J 1 e J 2 !! Sabendo que:

q i = E b i - J i 1 - ε i ε i A i

Isolando J i :

J i = E b i - q i A i 1 - ε i ε i      

Substituindo para achar J 1 e J 2 :

J 1 = 5,67 × 10 - 8 × 1000 4 - 9874 × 1 - 0,33 0,33 = 36,643   W / m 2

J 2 = 5,67 × 10 - 8 × 700 4 - 9874 × 1 - 0 , 5 0 , 5 = 23,488     W / m 2

Podemos achar T 3 :

T 3 = 36,643 + 23,488 2 × 5,67 × 10 - 8 1 4

Calculando:

T 3 = 853   K

Passo 6

E pra acabar, vamos discutir a influência de ε 3 nos resultados!!!

Eu não sei se você reparou, mas nós não usamos esse dado em momento nenhum! Isso porque a superfície é rerradiante, então se variarmos ε 3 a gente não vai ter nenhuma mudança!

E será que as aproximações que a gente consiiderou são rasoáveis?!

Consideramos por exemplo uma radiosidade uniforme saido de todas as superfícies! Mas concorda que para os cantos por exemplo isso não é verdade?!

Para um resultado mais preciso, poderiamos ter subdividido as regiões!

Agora acabou!! Uhuuuul!!!

Resposta

q 1 ' = 9874   W / m

T 3 = 853   K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Silício sólido puro é produzido a partir de material fundido, como por exemplo, no Problema 1.37. Silício sólido é semitransparente e a distribuição do coeficiente de absorção espectral para o silício
Considere um forno circular que tem 0,5m de comprimento e 0,5m de diâmetro. As duas extremidades têm superfícies cinzas e difusas, que são mantidas a 400 e 500K , com emissividades de 0,4 e 0,5 , resp
Um forno que tem uma cavidade esférica com 0,4m de diâmetro contém uma mistura gasosa a 1a t m e 1400K . A mistura é formada por C O 2 , com uma pressão parcial de 0,25a t m , e nitrogênio com uma pre
Uma liga de alumínio fundida a 950K é despejada em um recipiente cilíndrico que é isolado termicamente de uma grande vizinhança a 300K . O diâmetro interno do recipiente é de 500m m e a distância do l
Um secador de grãos é constituído por um longo duto semicircular com raio R = 1m . Metade da superfície da base é ocupada por uma placa eletricamente aquecida, com emissividade ε p = 0,8 , enquanto a