Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 2.Exercício - Ex. 36
A comporta da figura, articulada no extremo , mantém-se na condição de equilíbrio pela ação da força aplicada em . Sendo e a largura da comporta igual a , determinar o valor de e o da força vertical que solicita a articulação em .
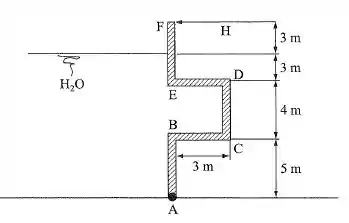
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Temos os seguintes prismas de pressão gerado na comporta. Cada um pode ser representado como uma força pontual a qual usaremos para determinar .
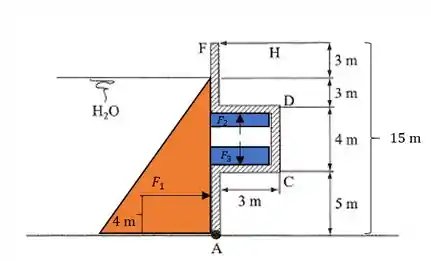
Sabemos que a força é igual ao volume do prisma de pressão. Portanto:
Como:
Temos que:
Temos também que:
E:
Passo 2
A condição de equilíbrio é de que o somatório de momentos no ponto é zero. Portanto:
A reação vertical em é encontrada a partir do somatório de forças verticais no sistema:
Resposta
Exercícios de Livros Relacionados
Uma placa plana horizontal submersa é suspensa na água por uma corda anexada ao centróide de sua superfície superior. Agora a placa é girada a 45 ° com relação a um eixo que passa através de seu centr
Uma pessoa diz que pode determinar a intensidade da força hidrostática que age sobre uma superfície plana submersa na água, independente da forma e orientação, se ela conhecer a distância vertical do
Diz-se que Arquimedes descobriu seu princípio durante um banho enquanto pensava sobre como poderia determinar se a coroa do rei Hiero era feita realmente de ouro puro. Enquanto estava na banheira, ele
Sob quais condições um corpo móvel de fluido pode ser tratado como um corpo rígido?
O casco de um barco tem um volume de 150m 3 , e a massa total do barco vazio é 8560k g . Determine quanta carga esse barco pode carregar sem afundar ( a ) em um lago e ( b ) na água do mar com uma den