Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 2.Exercício - Ex. 37
Um cilindro de ferro fundido, de de diâmetro e de altura, é imerso em água do mar . Qual é o empuxo que a água exerce no cilindro? Qual seria o empuxo se o cilindro fosse de madeira ? Nesse caso, qual seria a altura submersa do cilindro?
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão… Primeiro ela quer o empuxo no cilindro de ferro fundido, depois quer esse empuxo mudando o material do cilindro para madeira e por último pede a altura submersa dele se fosse de madeira… Hum… Coisa pra caramba, né? Mas relaxa que a gente dá conta disso!
Bom, o empuxo é dado pelo produto do peso específico do fluido pelo volume submerso. No primeiro caso, o cilindro está totalmente imerso na água do mar, portanto:
Como o volume do cilindro é dado pelo produto da área da base pela altura, temos que:
E a base do cilindro é uma circunferência, então vamos ter:
Substituindo os valores dados no enunciado, temos que:
Opa! Já resolvemos a primeira parte!
Passo 2
Agora vamos para o segundo caso, onde o cilindro é de madeira. Nesse caso, vamos pensar… A madeira vai ficar submersa quando o empuxo for igual a força peso que está atuando sobre o cilindro, certo? Então ficamos com:
E podemos calcular esse peso, fazendo:
E como o empuxo é igual a força peso, teremos:
Show de bola! Agora só falta encontrar a última parte!
Passo 3
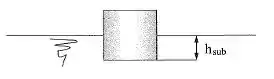
Para saber qual a altura submersa do cilindro de madeira em água, vamos usar a relação:
Isolando a altura, temos:
Prontinho!
Resposta
Empuxo no caso do cilindro ser de ferro fundido:
Empuxo no caso do cilindro ser de madeira:
Altura submersa do cilindro de madeira: