Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 2.Exercício - Ex. 40
Um sistema de bóia é utilizado para abrir um reservatório de água quando o nível deste atinge o plano diametral da esfera. Calcular a área do disco de fechamento do reservatório, sabendo que a área da seção transversal da haste é e o peso do conjunto (esfera, haste e disco) é . Dados: ; ; .
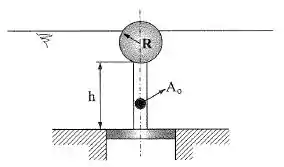
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
A condição de equilíbrio é a de que o empuxo seja igual a força que a água causa no disco somada do peso do sistema .
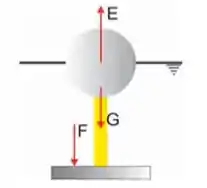
Sabemos que o empuxo é dado pelo produto do peso específico pelo volume submerso.
Como nos foi dito que a condição limite é quando o nível de liquido atinge o plano diametral, que é aquele que passa pelo diâmetro, temos que o volume submerso será a metade da esfera menos o volume de contato da haste na parte inferior da esfera.
A força provocada pela água no disco é de:
E o peso total do sistema já nos foi dado.
Passo 2
Organizando os dados do passo anterior, temos que:
Como a pressão e a altura total é de , temos que:
Substituindo os valores conhecidos, temos que:
Sendo a área a área do disco menos a área da seção transversal da haste . Portanto: