Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Sistemas de Controle - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 71

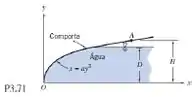
A comporta mostrada tem 1,5 m de largura e é articulada em O; a   =   1,0   m – 2 , D   =   1,20   m e H   =   1,40   m . Determine (a) o módulo e o momento da componente vertical da força em torno de O, e (b) a força horizontal que deve ser aplicada em torno do ponto A para manter a comporta na posição mostrada.

Passo 1

Nessa questão temos um portão parabólico, articulado em O , o qual possui uma largura constante. Vamos encontrar a magnitude e momento da força vertical no portão devido à água, e a força horizontal aplicada em A   necessária para manter o equilíbrio

Para resolução, aplicaremos as equações hidrostáticas a seguir:

d p d h = ρ g , pressão hidrostática

∑ M = 0 , equilíbrio de rotação

F v = ∫ p d A y , força hidrostática vertical

x ' F v = ∫ x d F v , momento de força vertical

y ' F H = ∫ y d F H , momento de força horizontal

Como todo problema da MecFlu, fazemos as seguintes considerações: fluido estático e incompressível; pressão atmosférica atua na superfície livre da água e fora do portão.

Passo 2

Começamos sempre integrando a equação da pressão hidrostática. Assim, para o item (a) temos:

F v = ∫ p d A y = ∫ ρ g h b d x

Onde: H = D - y , x = a y 3 , d x = 3 a y 2 d y .

Substituindo de volta à relação pela força:

∫ 0 D ρ g D - y b 3 a y 2 d y = 3 ρ g b a ∫ 0 D D y 2 - y 3 d y

Calculando a integral:

F v = 3 ρ g b a D 4 3 - D 4 4 = ρ g b a D 4 4

Agora, substituindo os valores:

F v = 999 k g m 3 × 9,81 m s 2 × 1,5   m × 1 m 2 × ( 1,2   m ) 4 4

F v = 7,62   k N

Para encontrar o momento, usamos a derivação da força:

x ' F v = ∫ x p d A y

x ' F v = ∫ 0 D a y 3 ρ g   D - y b 3 a y 2 d y

x ' F v = 3 ρ g a 2 b ∫ 0 D D y 5 - y 6 d y

x ' F v = 3 ρ g a 2 D 7 6 - D 7 7 = 3 42 ρ g a 2 b D 7 = ρ g a 2 b D 7 14

Substituindo os valores:

x ' F v = 999 k g m 3 × 9,81 m s 2 × 1 m 2 2 × 1,5   m × ( 1,2   m ) 7 14

x ' F v = 3,76   k N × m

Passo 3

Agora para a força horizontal em A , tomamos os momentos em O :

x ' F v + y ' F H - H F A = 0

Resolvendo a força em A :

F A = 1 H   x ' F v + y ' F H

Para obter o momento da força hidrostática horizontal:

y ' F H = ∫ y d F H

y ' F H = ∫ y p d A x

y ' F H = ∫ y ρ g h b d y = ρ g b ∫ 0 D D y - y 2 d y

Resolvendo a integral:

y ' F H = ρ g b D 3 2 - D 3 3 = ρ g b D 3 6

Substituindo os valores:

y ' F H = 999 k g m 3 × 9,81 m s 2 × 1,5   m × 1,2 3 6 = 4,23   k N × m

Então a força F A é:

F A = 1 1,4 3,76   k N × m + 4,23   k N × m

F A = 5,71   k N

Prontinho!!

Resposta

(a) F v = 7,62   k N e x ' F v = 3,76   k N × m

(b)   y ' F H = 4,23   k N × m e F A = 5,71   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A comporta mostrada na figura tem 3 m de largura e, para fins de análise, pode ser considerada sem massa. Para qual profundidade de água esta comporta retangular ficará em equilíbrio como mostrado?
Uma grande tora cilíndrica de madeira, com diâmetro D , apoia-se contra o topo de uma barragem. A água está nivelada com o topo da tora e o centro dessa está nivelado com o topo da barragem. Obtenha e
Considere uma caneca de chá (com 65 mm de diâmetro). Imagine a caneca cortada simetricamente ao meio por um plano vertical. Encontre a força que cada metade experimenta devido a coluna de 80 mm de chá
Uma portinhola triangular de acesso deve ser projetada para ser colocada na lateral de uma forma contendo concreto líquido. Usando as coordenadas e dimensões mostradas, determine a força resultante qu
Uma comporta de vertedouro, com a forma de um arco circular, tem w metros de largura. Determine o módulo e a linha de ação da componente vertical da força devida a todos os fluidos atuando sobre a com