Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Sistemas de Controle - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 81

Uma grande tora cilíndrica de madeira, com diâmetro D , apoia-se contra o topo de uma barragem. A água está nivelada com o topo da tora e o centro dessa está nivelado com o topo da barragem. Obtenha expressões para (a) a massa da tora por unidade de comprimento e (b) a força de contato entre a tora e a barragem por unidade de comprimento.

Passo 1

Esse probleminha é sobre uma tora cilíndrica flutuando contra barragem, nele temos que encontrar duas coisinhas: a massa por unidade de comprimento do tronco e a força de contato por unidade de comprimento entre o tronco e a barragem.

Aplicaremos as equações hidrostáticas neste sistema, que são:

d p d h = ρ g

d F → = p d A →

Para facilitar a visualização, temos o seguinte diagrama de corpo livre:

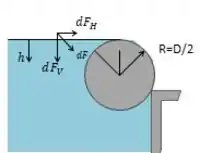
Como todo e qualquer problema da MecFlu, temos as seguintes considerações: fluido estático e incompressível; e a pressão atmosférica atua em superfícies livres e no primeiro quadrante da tora.

Passo 2

Para inicio de resolução, vamos integrar a equação da pressão hidrostática:

p = ρ g h   =   ρ g R ( 1 - cos ⁡ θ )

Agora, vamos organizar as forças horizontais e verticais:

d F = p d A = p w R d θ = ρ g R 1 - cos ⁡ θ w R d θ = ρ g R 2 w 1 - cos ⁡ θ

d F H = d F sin ⁡ θ = ρ g R 2 w 1 - cos ⁡ θ d θ sin ⁡ θ

d F V = d F cos ⁡ θ = ρ g R 2 w 1 - cos ⁡ θ d θ cos ⁡ θ

Se integrarmos a força horizontal teremos a força de contato por unidade de comprimento:

F H = ∫ 0 3 π 2 ρ g R 2 w 1 - cos ⁡ θ sin ⁡ θ d θ

= ρ g R 2 w ∫ 0 3 π 2 sin ⁡ θ - sin ⁡ θ cos ⁡ θ d θ

= ρ g R 2 w - 1 2 + 1 ∴ F H = ρ g R 2 w 2

Então, a relação entre a força e o comprimento é de: F H w = ρ g R 2 2 .

Agora, se integrarmos para a força vertical, teremos a massa por unidade de comprimento da tora:

F V = ∫ 0 3 π 2 ρ g R 2 w 1 - cos ⁡ θ cos ⁡ θ d θ

= ρ g R 2 w ∫ 0 3 π 2 cos ⁡ θ - cos ⁡ θ cos ⁡ θ d θ

= ρ g R 2 w - 1 - 3 π 4

Então, a relação entre a força e o comprimento é de: F V w = - ρ g R 2 1 + 3 π 4 .

Para descobrirmos a massa, fazemos a analise de forças pelo diagrama de corpo livre:

∑ F y = 0

- m w g - F V w = 0

m w = - F V w g

Substituindo a força vertical, temos:

m w = ρ R 2 1 + 3 π 4

Prontinho!!

Resposta

  1. m w = ρ R 2 1 + 3 π 4
  2. F H w = ρ g R 2 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A comporta AOC mostrada na figura tem 1,8 m de largura e é articulada em O. Desconsiderando o peso da comporta, determine a força na barra AB. A comporta é vedada em C.
A comporta retangular mostrada na figura abrese automaticamente, quando o nível da água no seu lado esquerdo atinge uma determinada altura. A que profundidade acima da articulação isto acontece? Despr
Para a geometria mostrada, qual é a força vertical sobre a represa? Os degraus têm 0,5 m de altura, 0,5 de profundidade e 3 m de largura.
Para a geometria mostrada, qual é a força vertical da água sobre a represa?
A comporta mostrada na figura tem 3 m de largura e, para fins de análise, pode ser considerada sem massa. Para qual profundidade de água esta comporta retangular ficará em equilíbrio como mostrado?