Enunciado
Sistemas de Controle - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 65
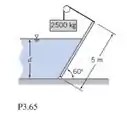
A comporta mostrada na figura tem 3 m de largura e, para fins de análise, pode ser considerada sem massa. Para qual profundidade de água esta comporta retangular ficará em equilíbrio como mostrado?
Passo 1
No problema, temos o portão mostrado com largura fixa de 3 metros (chamaremos de ). Podemos dizer que a parte de baixo do portão é insignificante e que o mesmo está em equilíbrio.
Para resolvermos, precisamos encontrar a profundidade da água e para isso aplicaremos as equações hidrostáticas neste sistema, são elas
, referente a pressão hidrostática ( é positivo para baixo)
, equilíbrio rotacional
, força hidrostática
, a localização da linha de ação
Fazemos algumas considerações: fluido estático; fluido incompressível; A pressão atmosférica atua na superfície livre da água e fora do portão.
O diagrama que representa esse sistema é o seguinte:
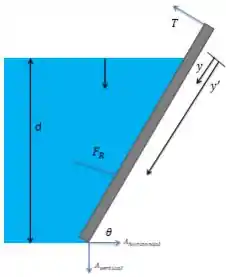
Passo 2
O ponto inicial é dado integrando a equação da pressão hidrostática:
Nesse caso, a altura é a metade de , ou seja, e a área é . Logo,
Para encontrar a linha de força, temos
, onde
onde é o comprimento do portão em contato com a água (conforme o diagrama). Logo,
Dessa forma, e se relacionam, logo,
Portanto,
Assim, substituindo na formula da linha de força, obtemos
Passo 3
Feito todas essas analises podemos avaliar as forças do diagrama mostrado no inicio (tendo cuidado com os sinais),
Onde .
Isolamos, então
Assim, colocamos em evidencia a variável :
Logo,
Substituindo os dados, vamos obter o seguinte resultado:
Prontinho!!