Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Sistemas de Controle - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 75

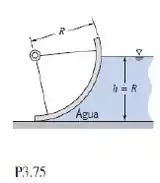
Uma comporta de vertedouro, com a forma de um arco circular, tem w metros de largura. Determine o módulo e a linha de ação da componente vertical da força devida a todos os fluidos atuando sobre a comporta.

Passo 1

Nessa questão temos um portão com um formato de arco circular. Devemos calcular o módulo e a linha de ação da componente vertical da força. Agora vamos ver com quais expressões podemos calcular isso:

d p d h = γ , pressão hidrostática onde h é positivo para baixo.

F v = - ∫ p d A y , força hidrostática vertical

x ' F V = ∫ x d F V

Como todo problema da MecFLu, fazemos algumas considerações: fluido estático e incompressível; pressão atmosférica atuando na superfície da agua e fora do portão.

Passo 2

Vamos começar integrando a equação da pressão hidrostática. Usaremos θ como nossa variável de integração, logo y = R sin ⁡ θ e o diferencial de área será:

d y = R cos ⁡ θ   d θ     ∴ d A y = w R sin ⁡ θ d θ

Assim, podemos aplicar na equação:

F v = - ∫ p d A y

F v = - ∫ 0 π 2 ρ g R sin ⁡ θ w R sin ⁡ θ d θ

= - ρ g R 2 w ∫ 0 π 2 sin ⁡ θ 2 d θ

F V = - ρ g R 2 w π 4

Passo 3

Para encontrarmos a linha de ação:

x ' F V = ∫ x d F V

Onde: x = R cos ⁡ θ e d F V = - ρ g R 2 w sin ⁡ θ 2   d x , então:

x ' = x ' F V F v = - 4 π ρ g R 2 w × ∫ 0 π 2 - R cos ⁡ θ ρ g R 2 w sin ⁡ θ 2 d θ

Resolvendo a integral, temos:

= 4 R p i ∫ 0 R sin ⁡ θ 2 cos ⁡ θ d θ

x ' = 4 R 3 π

Prontinho!!

Resposta

F V = - ρ g R 2 w π 4

x ' = 4 R 3 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma comporta Tainter, usada para controlar a vazão de água na represa de Uniontown no Rio Ohio, é mostrada na figura; a sua largura é w = 35 m. Determine o módulo, o sentido e a direção da linha de aç
Uma superfície curva é formada com um quadrante de um cilindro circular de raio R=0,750m , conforme mostrado. A superfície tem largura w=3,55m . Água permanece à direita da superfície até uma profundi
Uma barragem cilíndrica tem diâmetro de 3 m e comprimento de 6 m. Determine o módulo e o sentido da força resultante da água agindo sobre a barragem.
Uma comporta, na forma de um quarto de cilindro, articulada em A e vedada em B, tem 3 m de largura. O fundo da comporta está 4,5 m abaixo da superfície da água. Determine a força sobre o batente B, se
A comporta mostrada tem 1,5 m de largura e é articulada em O; a=1,0m – 2 , D=1,20m e H=1,40m . Determine (a) o módulo e o momento da componente vertical da força em torno de O, e (b) a força horizonta