Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Sistemas de Controle - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 73

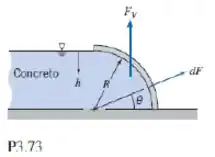
Concreto líquido é despejado na forma mostrada ( R   =   0,313   m ). A forma tem largura w   =   4,25   m normal ao diagrama. Calcule o módulo da força vertical exercida sobre a forma pelo concreto e especifique sua linha de ação.

Passo 1

Nessa questão temos concreto líquido sendo derramado conforme a figura mostra. Devemos calcular o módulo e a linha de ação da componente vertical da força. Agora vamos ver com quais expressões podemos calcular isso:

d p d h = ρ g , pressão hidrostática onde h é positivo para baixo.

F v = ∫ p d A y , força hidrostática vertical

x ' F V = ∫ x d F V

Como todo problema da MecFLu, fazemos algumas considerações: fluido estático e incompressível; pressão atmosférica atuando na superfície da agua e fora da parede.

Passo 2

Vamos começar integrando a equação da pressão hidrostática. A altura pode ser definida como h = R - y = R - R sin ⁡ θ A área também pode ser expressa por: d A = w R   d θ .

Assim, podemos aplicar na equação:

F v = ∫ p d A y

F v = ∫ 0 π 2 ρ g   R - R sin ⁡ θ w R sin ⁡ θ d θ

= ρ g w R 2 ∫ 0 π 2 [ sin ⁡ θ - sin ⁡ θ 2 ]   d θ

Substituindo os valores temos:

F V = ρ g w R 2 - 0 - 1 - π 4 - 0 + 0

F V = ρ g w R 2 1 - π 4

A densidade do coencreto é dada por: ρ = 2,5 × 999 k g m 3 = 2497,5   k g / m 3 , logo:

F V = 2497,5 k g m 3 × 9,81 m s 2 × 4,25   m × ( 0,313   m ) 2 1 - π 4

F V = 2189,2   N

Passo 3

Para encontrarmos a linha de ação:

x ' F V = ∫ x d F V

x ' F V = ∫ R cos ⁡ θ ρ g R - R sin ⁡ θ w R sin ⁡ θ d θ

= ρ g w R 3 ∫ 0 π 2 [ sin ⁡ θ cos ⁡ θ - sin ⁡ θ 2 cos ⁡ θ ]   d θ

Resolvendo a integral, temos:

x ' F V = ρ g w R 3 1 2 - 1 3  

Então:

x ' = x ' F V F v = ρ g w R 3 1 2 - 1 3 ρ g w R 2 1 - π 4 = R 6 1 - π 4

x ' = 0 , 243   m

Prontinho!!

Resposta

F V = 2189,2   N

x ' = 0,243   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma comporta retangular (de largura w = 2 m) é articulada conforme mostrado, com um batente na borda inferior. Em que profundidade H a comporta estará prestes a abrir?
Uma comporta plana semicircular AB, articulada ao longo de B, é suportada pela força horizontal FA aplicada em A. O líquido à esquerda da comporta é água. Calcule a força FA requerida para o equilíbri
Uma represa deve ser construída usando a seção transversal mostrada. Suponha que a largura da represa seja w = 50 m. Para uma altura de água H = 2,5 m calcule o módulo e a linha de ação da força verti
A comporta parabólica mostrada na figura tem 2 metros de largura e é articulada em O ; c = 0,25m - 1 , D = 2m e H = 3m . Determine (a) o módulo e a linha de ação da força vertical sobre a comporta cau
Uma sólida represa de concreto deve ser construída de modo a reter água até uma profundidade D . Para facilitar a construção, as paredes da represa devem ser planas. Sua supervisora solicita que você