Uma seção de parede vertical deve ser construída com mistura pronta de concreto derramada entre formas. A seção de parede tem 3 m de altura, 0,25 m de espessura e 5 m de largura. Calcule a força exercida pelo concreto sobre cada forma. Determine a linha de aplicação da força.

Bom, pra começo de conversa o que temos a resolver é a força exercida sobre o concreto. Nesse exercício de estática dos fluidos, consideramos aqui que a densidade é um valor tabelado equivalente a . Logo, .

Para a resolução precisaremos de algumas equações da hidrostática, as seguintes:

E agora, é necessário saber em qual linha aquela força vai ser aplicada, por isso chamamos de e . Analisamos a figura e verificamos as equações:

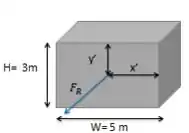
é equivalente ao momento de inercia em cada linha. Portanto, e (porque é perpendicular).

Como é equivalente a e a , então os valores são, respectivamente, e .