Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 9.Problemas - Ex. 32

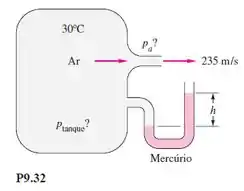
O ar comprimido de um grande tanque (Figura P9.32) escapa por um bocal a uma velocidade de saída de 235 m/s. O manômetro de mercúrio mede h = 30   c m . Admitindo escoamento isentrópico, calcule a pressão (a) no tanque e (b) na atmosfera. (c) Qual é o número de Mach na saída?

Passo 1

E lets go, bora lá!

Bora ver qual a temperatura de saída, tendo R = 287   J / k g K e k = 1,4 , assim:

T e = T 0 - V e 2 2 c p = 303   K - 235 m s 2 2 k R k - 1 = 276   K

Logo,

M a e = V e a e = V e k R T e = 232 m s 1,4 287 J k g K 276   K = 0,706

Já encontramos (c), isso porque vamos precisar desse Mach.

Passo 2

Teremos que:

p t a n q u e p e = 1 + 0,2 M a e 2 3,5 = 1,395

E,

p t a n q u e - p e = ρ H g - ρ t a n q u e g h

Estimando ρ t a n q u e = 1,6   k g / m 3 , teremos:

p t a n q u e - p e = 13550 k g m 3 - 1,6 k g m 3 9,81 m s 2 0,30   m = 39900   P a

A partir das equações, conseguiremos chegar em

p e = 101   k P a

e

p t a n q u e = 140,8   k P a

Resposta

  1. 140,8 kPa
  2. 101 kPa
  3. 0,706
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um certo volume de gás nitrogênio inicialmente a 60k P a e 7° C entra em um difusor adiabático em regime permanente a uma velocidade de 275m / s , saindo a 85k P a e 27° C . Determine ( a ) a velocida
A energia cinética de um fluido aumenta à medida que ele e acelerado em um bocal adiabático. De onde vem essa energia?
Um difusor e um dispositivo adiabático que diminui a energia cinética do fluido, pela sua desaceleração. O que acontece a essa energia cinética perdida?
Vapor de água a 4 MPa e 400 °C entra em um bocal em regime permanente com uma velocidade de 60 m/s, e sai a 2Mpa e 300 °C. A área na entrada do bocal é de 50 c m 2 e calor está sendo perdido a uma tax
Vapor entra um tubo isolado a 200 kPa e 200 °C e sai a 150 kPa e 150 °C. A relação de diâmetros de entrada a saída para o tubo é D1/D2 =1,80. Determine as velocidades de entrada e saída do vapor.