Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 5.Problemas - Ex. 113

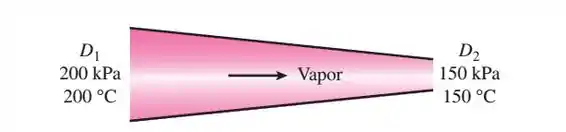
Vapor entra um tubo isolado a 200 kPa e 200 °C e sai a 150 kPa e 150 °C. A relação de diâmetros de entrada a saída para o tubo é D1/D2 =1,80. Determine as velocidades de entrada e saída do vapor.

Passo 1

O primeiro passo da questão é obter as propriedades do vapor em P 1 = 200   k P a e T 1 = 200 º   C na tabela A - 6 “Água, vapor superaquecido” na página 918.

Entalpia específica: h 1 = 2870,7   k J / k g

Volume específico: v 1 = 1,0805   m 3 / k g  

Passo 2

Obtendo as propriedades para o vapor em P 2 = 150   k P a   e T 2 = 150 º C na mesma tabela, interpolando entre as pressões de 200   k P a e 100   k P a

h 2 = h 100   k P a + 150   k P a - 100   k P a 200   k P a - 100   k P a ⋅ h 200   k P a - h 100   k P a   h 2 = 2776,6 + 150 - 100 200 - 100 × 2769,1 - 2776,6 h 2 = 2772,85   k J / k g

v 2 = v 100   k P a + 150   k P a - 100   k P a 200   k P a - 100   k P a ⋅ v 200   k P a - v 100   k P a   v 2 = 1,9367 + 150 - 100 200 - 100   0,95986 - 1,9367 v 2 = 1,44828   m 3 / k g

Passo 3

Consideramos como volume de controle como o tubo, já que a massa atravessa a fronteira. Como há apenas uma entrada e uma saída, a massa que entra é a mesma massa que sai:

m 1 = m 2 A 1 V 1 v 1 = A 2 V 2 v 2 π 4 × D 1 2 V 1 v 1 = π 4 × D 2 2 V 2 v 2 V 1 = v 1 v 2 × D 2 2 D 1 2 × V 2   ( 1 )

Em que V 1 , V 2 , D 1 , D 2 são as velocidades e diâmetros de entrada e saída respectivamente

Substituindo D 2 D 1 = 1 D 1   D 2 = 1 1,8 , v 1 = 1,0805   m 3 / k g e v 2 = 1,44828   m 3 / k g para achar a relação entre V 1   e   V 2   na equação (1):

V 1 = 1,0805 1,44828 × 1 1,8 2 × V 2 V 1 = 0,23026 ⋅   V 2

Passo 4

Agora iremos aplicar a conservação de energia para o sistema

Para um sistema em regime permanente, a energia armazenada dentro do sistema é zero.

E ˙ e n t r a d a = E ˙ s a í d a h 1 + V 1 2 2 = h 2 + V 2 2 2

Substituindo h 1 = 2870,7   k J / k g , h 2 = 2772,85   k J / k g e V 1 = 0,23026 V 2 :

2870,7 k J k g + 0,23026 V 2   m / s 2 2   1 k J k g 1000 m 2 s 2 = 2772,85 + V 2   m / s 2 2   1 k J k g 1000 m 2 s 2 V 2   m / s 2 2 000 - 0,23026 V 2 m s 2 2 000 = 2870,7 k J k g - 2772,85

V 2 2 - 0,053 V 2 2 2000 = 97,85 1 - 0,053 V 2 2 2000 = 97,85 V 2 2 = 2000 × 97,85 1 - 0,053 V 2 =     2000 × 97,85 1 - 0,053 V 2 = 454,6   m / s

Passo 5

Com o valor de V 2 podemos calcular V 1 diretamente:

Portanto V 1 = 0,23026 × 454,59 = 104,67   m / s

Resposta

V 1 = 104,67   m / s V 2 = 454,6   m / s  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os estatores em uma turbina a gás são concebidos para aumentar a energia cinética do gás que passa adiabaticamente por eles. Ar entra em um conjunto desses bocais a 300p s i a e 700° F com uma velocid
Refrigerante-134a entra em regime permanente em um difusor como vapor saturado a 800k P a com velocidade de 120m / s e sai a 900k P a e 40° C . O refrigerante esta ganhando calor a uma taxa de 2k J /
O difusor de um motor a jato e projetado para diminuir a energia cinética do ar que entra no compressor sem nenhuma interação de trabalho ou calor. Calcule a velocidade da saída do ar no difusor quand
Vapor entra em um bocal a 400° C e 800k P a com uma velocidade de 10m / s e sai a 300° C e 200k P a , enquanto perde calor a uma taxa de 25k W . Para uma area de entrada de 800c m 2 , determine a velo
Ar a 13p s i a e 50° F entra em um difusor adiabatico em regime permanente com velocidade de 600p e s / s e sai com baixa velocidade a uma pressão de 14,5p s i a . A area de saida do difusor e quatro