Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 39

A condutividade térmica e a emissividade da superfície de um material podem ser determinadas pelo aquecimento de sua superfície inferior e exposição de sua superfície superior ao ar quiescente e a uma grande vizinhança com temperaturas equivalentes, T∞ = Tviz = 25°C. As superfícies restantes da amostra/aquecedor são bem isoladas.

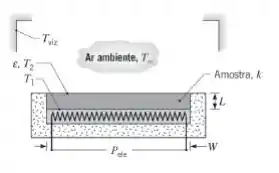
Considere uma amostra com espessura L = 25 mm e uma plataforma quadrada de largura W = 250 mm. Em um experimento realizado sob condições de regime estacionário, medidas de temperatura efetuadas nas superfícies inferior e superior da amostra fornecem os valores T1 = 150°C e T2 = 100°C, respectivamente, para uma alimentação de potência de Pele = 70 W. Quais são a condutividade térmica e a emissividade da amostra?

Passo 1

Fala aí! Vamos fixar nossos conhecimentos resolvendo esse probleminha? Vamos nessa!

O enunciado quer da gente a emissividade e a condutividade térmica nessas condições aí… Então vamos dar isso a ele!

Mas antes vamos anotar nossos dados, beleza?

L = 25   m m   W = 250   m m T ∞ = 25 ° C

T s u r = 25 ° C T 1 = 150 ° C T 2 = 100 ° C

Opa! Precisaremos de dados adicionais para o nosso cálculo, vamos encontrar eles no apêndice do livro, tabela A-4, assumindo um T f = 335,5   K :

k = 0,0289   W / m . K v = 19,5   .   10 - 6   m ² / s α = 27,8   .   10 - 6   m ² / s

P r = 0,703 β = 0,00298   K - 1

Vamos as continhas então!

Passo 2

Vamos começar encontrando o nosso k :

k = P e l e c / W ² T 1 - T 2 / L

k = 70 / 0,250 ² 50 / 0,025

k = 0,560   W / m . K

Agora para encontrar h _ , precisamos saber alguns fatores antes, como o R a L :

R a L = g   .   β   .   T s - T ∞   .   L ³ v   .   α

Mas nós não temos o L , vamos achar ele:

L = A s P = W ² 4   .   W

L = W 4

L = 0,250 4

L = 0,0625   m

Agora sim, voltaremos a equação ali de cima:

R a L = 9,8   .   0,00298   .   150 - 25   .   0,0625 ³ 19,5   .   10 - 6   .   27,8   .   10 - 6

R a L = 9,86   .   10 5

E por fim teremos o nosso h _ D :

h _ = N u _ L   .   k L = k L   .   0,54   .   R a L 1 / 4

h _ = 0,0289 0,0625   .   0,54   .   ( 9,86   .   10 5 ) 1 / 4

h _ = 7,87   W / m ² . K

Passo 3

Agora simmm… Vamos achar nosso ε com a seguinte relação:

P e l e c = q c o n v + q r a d

P e l e c = h _   .   T 2 - T ∞ + ε   .   σ   .   T 2 4 - T s u r 4   .   W ²

ε = P e l e c W ² - h _   .   T 2 - T ∞ σ   .   T 2 4 - T s u r 4

ε = 70 0,250 ²   -   7,87   .   75 5,67   .   10 - 8   .   373 4 - 298 4

ε = 0,815

Uhul! Conseguimos!!

Resposta

k = 0,560   W / m . K ε = 0,815

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma caixa de gelo cujas dimensões externas são 30 cm x 40 cm x 40 cm é feita de isopor ( k = 0,033 W/m.K) de 3 cm de espessura. Inicialmente, a caixa é preenchida com 35 kg de gelo a 0°C, e a temperat
Duas esferas concêntricas com raios de 5 cm e 10 cm estão tendo as temperaturas de superfície mantidas a 200°C e 100°C, respectivamente. O espaço entre as duas superfícies esféricas concêntricas é pre
Um tanque esférico de 4 m de diâmetro contém água com gelo a 0°C. O tanque é de casca fina, portanto a temperatura da superfície externa pode ser considerada igual à temperatura da água com gelo no in
Um grupo de 25 transistores de potência, que dissipa 1,5 W cada, é resfriado e fixado em uma placa quadrada de alumínio anodizada de preto montada na parede de uma sala a 30°C. A emissividade das supe
Os componentes de um sistema eletrônico que dissipa 180 W estão localizados em um duto horizontal de 1,2 m de comprimento cuja seção transversal é de 15 cm x 15 cm. Os componentes no duto são refriger