Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 9.Problemas - Ex. 123
Uma caixa de gelo cujas dimensões externas são 30 cm x 40 cm x 40 cm é feita de isopor (0,033 W/m.K) de 3 cm de espessura. Inicialmente, a caixa é preenchida com 35 kg de gelo a 0°C, e a temperatura da superfície interna da caixa de gelo pode ser considerada de 0°C o tempo todo. O calor de fusão da água a 0°C é 333,7 kJ/kg, e o ar ambiente ao redor está a 20°C. Ignorando qualquer transferência de calor a partir da base da caixa de gelo de 40 cm x 40 cm, determine quanto tempo demora para que o gelo na caixa derreta completamente, considerando que a caixa de gelo está sujeita (a) ar calmo e (b) ventos de 50 km/h. Considere o coeficiente de transferência de calor na parte da frente, de trás e na superfície superior como sendo o mesmo que nas superfícies laterais.
Passo 1
Vamos reunir nossas informações: temos 35 kg de gelo que serão derretidos. O calor de fusão é 333,7 kJ/kg. Temos também as dimensões da caixa 30 cm x 40 cm x 40 cm, sua espessura 3 cm e a condutividade do isopor 0,033 W/m.K. Sabemos, por fim, que a temperatura interna da caixa é 0°C e a temperatura do ar é 20°C. Ou, de uma forma mais visual:
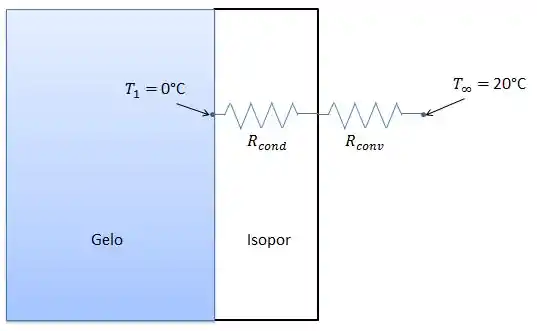
Então, basicamente o que temos são dois mecanismos de transmissão de calor envolvidos: condução e convecção (natural e/ou forçada). Vamos então: determinar a energia para derreter todo o gelo; calcular o coeficiente global para cada caso; encontrar a taxa de transferência de calor e, enfim calcular o tempo para que seja transferida a energia necessária para derreter todo o gelo. Pronto? Vamos nessa!!!
Então, como combinado nosso primeiro passo é calcular a energia para que todo o gelo se transforme em água líquida.
Vamos deixar assim por enquanto e depois voltaremos para encontrar o tempo.
Passo 2
Vamos considerar que as paredes do cilindro são placas planas de comprimento característico 30 cm. Para uma placa plana, com uma resistência condutiva e uma convectiva, o coeficiente global fica:
Sendo que é coeficiente convectivo de cada situação. Na letra (a) o ar é um vento calmo, então a convecção é natural. Antes de começar vamos assumir que o ar próximo à superfície tem temperatura do ambiente, ou seja, 20°C. As propriedas do ar nesta temperatura são:
A correlação de Nusselt para uma placa plana vertical é:
Precisamos dos adimensionais e . Já temos o número de Prandtl da tabela de propriedades do ar. Vamos para o número de Rayleigh:
Precisamos estimar uma temperatura para a superfície. Neste caso, como o isopor é um bom isolante, esperamos que a temperatura externa da placa seja mais próxima da do ar. Por isso, vamos considerar .
Já temos todas as variáveis necessárias para o número de Nusselt. Então vamos calcular :
O coeficiente global fica:
Vamos agora determinar a taxa de transferência de calor:
Antes de encontrar o tempo para derreter o gelo vamos verificar se a consideração de foi adequada. Caso encontemos uma temperatura muito diferente devemos estimar outro e recalcular tudo a partir do número de Rayleigh.
Para o mecanismo de convecção:
Que é próximo ao que estimamos. Vamos então para o cálculo do tempo:
Passo 3
Para o item (b) vamos prosseguir de maneira semelhante, mas agora o mecanismo de convecção é forçada. A velocidade do ar é km/h (que devemos transformar para m/s nos cáculos)Na convecção forçada sabemos que . Já temos o número de Prandtl do item anterior, então vamos calcular o número de Reynolds:
Para um escoamento sobre placa plana com :
O coeficiente global fica:
Vamos agora determinar a taxa de transferência de calor:
Por fim, vamos determinar o tempo para derreter todo o gelo:
Resposta
Ei, a resposta está no passo a passo :)