Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 15

A condutividade térmica k é uma medida da capacidade de um material de conduzir calor (Figura P7-15). Para a transferência de calor na direção x , através de uma superfície normal à direção x , a lei da condução de calor de Fourier é expressa como

Q ˙ c o n d u ç ã o = - k A d T d x

onde Q ˙ c o n d u ç ã o é a taxa de transferência de calor e A é a área normal à direção da transferência de calor. Determine as dimensões primárias da condutividade térmica k . Procure um valor de k nos apêndices e verifique se suas unidades S I são consistentes com seu resultado. Em particular, escreva as unidades S I primárias de 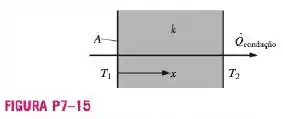k ,

Passo 1

Temos que determinar as unidades primárias de k e compará-las com as unidades do S I .

Determinando a fórmula de k :

Q ˙ c o n d u ç ã o = - k A d T d x

Isolando k :

k = Q ˙ c o n d u ç ã o A ∙ d T d x

Especificando o que é cada grandeza, Q ˙ c o n d u ç ã o é taxa de transferência de calor, ou seja, a quantidade de calor é transmitida por condução por unidade de tempo.

k = e n e r g i a t e m p o á r e a ∙ t e m p e r a t u r a c o m p r i m e n t o

Sabemos que área é multiplicação de comprimentos, com isto, vamos determinar energia em unidades primárias:

Passo 2

Determinando energia em unidades primárias:

E = j o u l e

Joules é unidade de energia, que é determinada pelo produto da força e espaço:

  j o u l e =   N e w t o n ∙   c o m p r i m e n t o

Para determinar Newton, temos:

N e w t o n = m a s s a ∙ a c e l e r a ç ã o  

N e w t o n = m a s s a ∙ c o m p r i m e n t o t e m p o 2

Substituindo por unidades primárias:

N e w t o n = m ∙ L t 2

Retomando o cálculo e substituindo Newton:

  j o u l e = m ∙ L t 2 ∙ L

J = m ∙ L 2 t 2

E = m ∙ L 2 t 2

Passo 3

Com o cálculo da energia, podemos determinar k em unidades primárias:

k = e n e r g i a t e m p o á r e a ∙ t e m p e r a t u r a c o m p r i m e n t o

Substituindo as unidades:

k = m ∙ L 2 t 2 t L 2 ∙ T L

k = 1 t ∙ m ∙ L 2 t 2 ∙ 1 L ∙ T

k = m L t 3 T

Passo 4

Temo que determinar k em unidades do S I :

k = e n e r g i a t e m p o á r e a ∙ t e m p e r a t u r a c o m p r i m e n t o

Para S I :

Unidade de comprimento é metro, unidade de tempo é segundos, unidade de temperatura é Kelvin, e unidade de energia precisa ser determinada:

Determinando a unidade de energia no S I , aproveitando todo o cálculo que já foi feito para energia

  j o u l e = m ∙ L t 2 ∙ L

Temos o produto de massa comprimento divididos pelo tempo, substituindo por unidade do S I :

Lembrando que para massa no S I seria k g .

j o u l e = k g ∙ m s 2 ∙ m = k g m 2 s 2

Passo 5

Retomando o cálculo de k no S I :

k = e n e r g i a t e m p o á r e a ∙ t e m p e r a t u r a c o m p r i m e n t o

Substituindo por unidade do S I :

k = k g m 2 s 2 s m 2 ∙ K m

k = k g m 2 s 2 ∙ 1 s ∙ 1 K ∙ m

k = k g ∙ m s 3 ∙ K

Resposta

Unidades primárias:

k = m L t 3 T

S I :

k = k g ∙ m s 3 ∙ K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Escreva as dimensões primárias de cada uma das seguintes variáveis da área da termodinâmica, mostrando todo o seu trabalho: ( a ) energia E ; b energia específica e = E / m ; c potência W ˙ .
Escreva as dimensões primárias da constante universal dos gases ideais, R u . (Sugestão: use a lei dos gases ideais, P V = n R u T , onde P é pressão, V é o volume, T é a temperatura absoluta e n é o
Em uma tabela periódica dos elementos, a massa molar M , também chamada p e s oa t ô m i c o ô , quase sempre é listada como se fosse uma quantidade adimensional (Figura P7-5). Na verdade, o p e s oa
Escreva as dimensões primárias de cada uma das seguintes variáveis do estudo da transferência de calor por convecção (Figura P7-16), mostrando todo o seu trabalho: a taxa de geração de calor g ˙ . (Di