Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 118

Uma configuração para dissipar calor de uma série de N = 100 circuitos integrados envolve a fixação dos circuitos à superfície inferior de uma placa e a exposição da superfície superior a um banho de água. O recipiente de água possui um lado com comprimento L = 100   m m e tem a sua superfície superior exposta a um escoamento de ar. O escoamento é tornado turbulento pela borda saliente da parede lateral do recipiente.

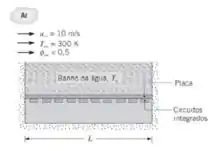
Se as laterais e a superfície inferior do recipiente são isoladas da vizinhança e o calor é dissipado uniformemente em cada circuito integrado, a que taxa pode o calor ser dissipado em cada circuito, com a temperatura da água mantida a T b = 350   K ?

Passo 1

Fala aí! Partiu resolver essa questão! Nosso enunciado quer saber a taxa de calor dissipado pelo circuito, show?

Vamos começar anotando todos os nossos dados:

u ∞ = 10   m / s L = 100   m m N = 100

T ∞ = 300   K φ ∞ = 0,5 T b = 350   K

Mas nós vamos precisar de mais dados do que isso, então vamos usar os anexos do livro, a tabela A-4, A-8 e A-6.

v B = 18,4 ×   10 - 6   m ² / s

P r = 0,704

S c = 0,622

D A B = 0,296 × 10 - 4   m ² / s

k = 0,0282   W / m . K

h f g = 2,32   × 10 6   J / k g

ρ g (   T b = 350   K ) = 0,260   k g / m ³

ρ g (   T ∞ = 300   K ) = 0,026   k g / m ³

Agora sim, temos tudo partiu fazer as continhas!

Passo 2

Pra gente achar a taxa de calor dissipado vamos usar essa equação aqui:

q 1 = L ² N   .   n A " + q "  

Precisamos encontrar alguns termos aí… O q " e n A " , mas antes de achar eles vamos fazer o seguinte:

h m _ = K L ⋅   0,037 ⋅   R e L 4 5 ⋅   P r 1 / 3

h _ m = D A B L   ⋅ 0,037 ⋅     R e L 4 5 ⋅ S c 1 / 3

Ops! Precisamos encontrar o número de Reynolds antes:

R e L = u ∞   .   L v B

R e L = 10   m / s   ×   0,1 m 18,4   .   10 - 6 m 2 / s

R e L = 54347.8

Show! Podemos voltar nas equações ali de cima então:

h m _ = 0,0282 0,1   ⋅ 0,037 ⋅ ( 54347.8 ) 4 5 ⋅ ( 0,704 ) 1 / 3

h _ m = 0,296   .   10 - 4 0,1   ⋅ 0,037   ⋅ ( 54347.8 ) 4 5 ⋅ ( 0,0622 ) 1 / 3

h _ = 57   W / m ²   .   K

h _ m = 0,0574   m / s

Agora sim, podemos encontrar o nosso n A " :

n A " = h _ m   . ρ g ( T b ) -   φ ∞   .   ρ g ( T ∞ ) ⋅ h f g

n A " = 0,0574   ⋅ 0,260 -   0,5   .   0,026 ⋅ 2.32 × 10 6

n A " = 34267.8   W / m 2

E o q " :

q " = h _   .   T b - T ∞

q " = 57   .   350 - 300

q " = 2850   W / m ²

Opa! Agora sim podemos encontrar a taxa de calor!

Passo 3

Vamos então para a última parte teremos:

q 1 = 0,1 ² 100   .   2850   W / m 2 + 34267.8     W / m 2

q 1 = 3.71   W

Uhul! Conseguimos!

Resposta

Portanto, a taxa de dissipação de calor de cada circuito é q 1 = 3,71   W .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

76. Um recipiente cilíndrico de paredes delgadas, com diâmetro D e altura L, contém, até uma altura y, um líquido (A) com baixo ponto de ebulição, que se encontra a Tsat,A. O recipiente está localizad
75. Uma seção de condensação–ebulição contém uma placa de cobre, com dimensões de 2 m × 2 m, que opera a uma temperatura uniforme de Ts = 100°C e separa vapor de água saturado, em condensação, de um l
74. Um esquema inovador para o resfriamento de chips de computadores utiliza um termossifão contendo um fluorocarboneto saturado. O chip é soldado no fundo de um recipiente com uma forma parecida com
66. O Ato do Ar Limpo (Clean Air Act) proibiu a produção de clorofluorocarbonos (CFCs) nos Estados Unidos a partir de 1996. Um CFC amplamente usado, refrigerante R-12, foi substituído pelo R-134a em m
68. Sejam as condições do Problema 10.67, mas agora com velocidade do vapor relativamente alta, com uma vazão mássica do fluido de = 2,5 kg/s.(a) Determine o coeficiente de transferência de calor e a