Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 10.Problemas - Ex. 68
68. Sejam as condições do Problema 10.67, mas agora com velocidade do vapor relativamente alta, com uma vazão mássica do fluido de = 2,5 kg/s.
(a) Determine o coeficiente de transferência de calor e a taxa de condensação por unidade de comprimento do tubo para uma fração mássica de vapor de X = 0,2.
(b) Represente graficamente o coeficiente de transferência de calor e a taxa de condensação para 0,1 ≤ X ≤ 0,3.
Passo 1
Letra (a)
Neste caso, como a fração mássica de vapor é de 0,2 nós devemos levar em consideração está informação e o desejado pela opção pode ser determinado como segue. Devemos ter em mente que como ele nos deu essa nova fração mássica o exercício não será resolvido exatamente como o anterior, mas sim com o uso de equações onde temos a fração de vapor levada em consideração.
Sendo assim, antes de começar a fazer os cálculos devemos obter as propriedades em 1,5 bar da tabela A.6, “Propriedades termo-físicas da água saturada”.
Temperatura saturada,
Calor latente de vaporização,
Densidade líquida da água,
Calor específico da água
Coeficiente de viscosidade,
A condutividade térmica do fluido é
Agora, devemos calcular qual é a vazão mássica por unidade de área dada da seguinte maneira:
A partir daí podemos utilizar a correlação de Dobson e Chato uma vez que o valor calculado é maior que o recomendado (
Sendo assim, podemos calcular o número de Reynolds pela seguinte formula:
Calculando o parâmetro de martinelli pela seguinte equação teremos:
Onde ao substituir os valores, chegaremos em:
Então, o número de Nusselt pode ser obtido a partir da seguinte correlação:
Sendo assim o coeficiente de transferência de calor é dado por:
Portanto, o coeficiente de transferência de calor é
A taxa de transferência de calor por unidade de comprimento é dada como:
Só que nesse caso não temos o calor latente modificado de vaporização. Com isso, podemos calcular o calor latente modificado pela seguinte fórmula:
A taxa de condensação por unidade de comprimento pode ser calculada pela seguinte fórmula:
Portanto, a taxa de condensação por unidade de comprimento é de .
Enfim, encontramos o que foi pedido no item a!!!!
Passo 2
Letra (b)
Neste caso, devemos repetir todos os cálculos feitos anteriormente escolhendo um valor para ir variando o X que neste caso foi de 0,05 dentro do intervalo estipulado. Após os cálculos utilizando o excel obtemos as seguintes tabelas com os valores do coeficiente de transferência de calor e taxa de condensação em função de X. E a cada tabela está assosiado um gráfico.
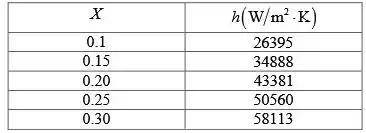
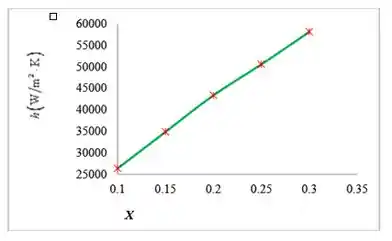
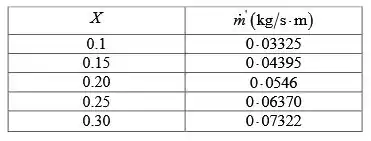
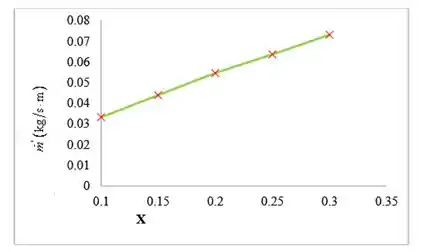
Resposta
- Gráficos e tabelas