Uma câmara cilíndrica de um reator nuclear de leito de partículas tem comprimento L = 10 m e diâmetro D = 3 m. A câmara abriga um leito composto por partículas esféricas de óxido de urânio com um núcleo de diâmetro Dp = 50 mm. Cada partícula gera energia térmica em seu núcleo a uma taxa Ėg e é coberta com uma camada de grafite, que não gera energia, e tem uma espessura uniforme δ = 5 mm. O óxido de urânio e o grafite possuem ambos uma condutividade térmica de 2 W/(m · K). O leito recheado possui uma porosidade ε = 0,40. Hélio pressurizado a 40 bar é usado para absorver a energia térmica das partículas. O hélio entra no leito recheado a Tent = 450°C com uma velocidade de 3,2 m/s. As propriedades do hélio podem ser consideradas como cp = 5193 J/(kg · K), k = 0,3355 W/(m · K), ρ = 2,1676 kg/m3 , μ = 4,214 × 10 −5 kg/(s · m) e Pr = 0,654.

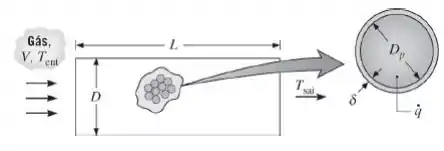
1. Para uma taxa de transferência de energia térmica global desejada de q = 125 MW, determine a temperatura média do hélio que deixa o leito, Tsai, e a quantidade de energia térmica gerada em cada partícula, Ėg.
2. A quantidade de energia gerada pelo combustível diminui se uma temperatura de operação máxima de aproximadamente 2100°C for ultrapassada. Determine a temperatura interna máxima da partícula mais quente no leito. Para números de Reynolds na faixa de 4000 ≤ ReD ≤ 10.000, a Equação 7.81 pode ser substituída por C = 2,876 ReD −1 + 0,3023 ReD −0,35 .

Podemos encontrar a taxa de transferência de energia térmica assim, olha só:

Ops! Precisamos encontrar esse :

Então nosso será:

Partiu letra b!

Vamos começar encontrando o número de Reynolds, ok?

Agora vamos encontrar o :

Agora podemos encontrar a temperatura :

E para achar o :

Vamos encontrar a temperatura máxima usando a equação de calor:

Precisamos encontrar essas constantes, então vamos usar nossas condições de contorno:

,

,

Vamos ter então que:

Precisamos encontrar esse aí, beleza?

E por fim teremos:

Uhull! Deu certo! Conseguimos!