Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 41
Considere ar atmosférico a = 2 m/s e = 300 K em escoamento paralelo sobre uma placa plana isotérmica de comprimento L = 1 m e temperatura = 350 K.
(a) Calcule o coeficiente convectivo local nas arestas frontal e de saída da placa aquecida, com e sem um comprimento inicial sem aquecimento de ξ = 1 m.
(b) Calcule o coeficiente convectivo médio na placa para as mesmas condições da parte (a).
(c) Represente graficamente a variação do coeficiente convectivo local ao longo da placa, com e sem um comprimento inicial sem aquecimento.
Passo 1
Vamos começar a letra (a) calculando a temperatura de filme, que será utilizada para calcular as propriedades de interesse do ar. Sabendo que ela é dada pela média entre e a temperatura de superfície, teremos:
Agora, com essa temperatura, vamos recorrer à tabela A.4 do apêndice A para encontrar as propriedades de interesse do ar, onde teremos:
Então, agora vamos calcular o número de Reynolds para o escoamento com o comprimento inicial sem aquecimento de , então, para o comprimento total, teremos:
Então, como temos o Reynolds crítico de , esse escoamento é laminar ao longo de toda a placa, com ou sem o comprimento inicial sem aquecimento.
Passo 2
Beleza, então, começando a análise sem o comprimento inicial sem aquecimento, iremos utilizar a seguinte correlação para Nusselt:
Então, substituindo os valores conhecidos, chegamos em:
E, sabendo que Nusselt se relaciona com o coeficiente convectivo através da seguinte equação:
Então, na aresta frontal, ou seja, em x = 0, teremos:
Agora iremos analisar a aresta de saída, nesse caso, o comprimento total é de 1 metro, então, substituindo os valores conhecidos nessa equação, chegamos em:
Passo 3
Agora vamos considerar o caso onde temos comprimento inicial sem aquecimento, nesse caso, iremos utilizar a seguinte correlação para Nusselt:
O termo é justamente a expressão para Nusselt sem o comprimento inicial sem aquecimento, que foi usada anteriormente, então, substituindo a expressão para Nusselt, essa equação se torna:
Então, para a aresta de entrada, ou seja, em x = 1, teremos:
E, dessa forma, o coeficiente convectivo será:
Agora, calculando Nusselt para a aresta de saída, ou seja, em x = 2 m, lembrando que nesse caso, o Reynolds utilizado será o do comprimento total de 2 m, ou seja, duas vezes aquele calculado no passo 1, então teremos:
E, substituindo esse valor na equação para o coeficiente convectivo, chegamos em:
Passo 4
Agora para a letra (b), precisamos calcular o coeficiente convectivo médio para os dois casos abordados na letra (a). Esse coeficiente convectivo médio pode ser encontrado através da equação 6.14, dada por:
Então, conforme vimos nos passos anteriores, o coeficiente convectivo pode ser escrito em função de Nusselt, dado por:
E, vimos também as equações utilizadas para Nusselt nos dois casos. Dessa forma, substituindo a correlação sem o comprimento inicial sem aquecimento, chegamos em:
E, por fim, substituiremos a relação para Reynolds nessa equação, chegando em:
Então, substituindo essa expressão na integral, chegamos em:
Resolvendo essa integral, chegamos em:
Substituindo os valores conhecidos, chegamos em:
Passo 5
Agora vamos repetir o processo do passo 4, só que com o comprimento inicial sem aquecimento, então, o coeficiente convectivo médio será:
Então, conforme vimos nos passos anteriores, o coeficiente convectivo pode ser escrito em função de Nusselt, dado por:
Substituindo a relação para Nusselt com o comprimento inicial sem aquecimento, teremos:
E, substituindo a expressão para Reynolds, temos:
E, substituindo essa relação na integral lá de cima, teremos:
Resolvendo essa integral com o auxílio de uma calculadora, chegamos no seguinte valor para o coeficiente de convecção médio:
Passo 6
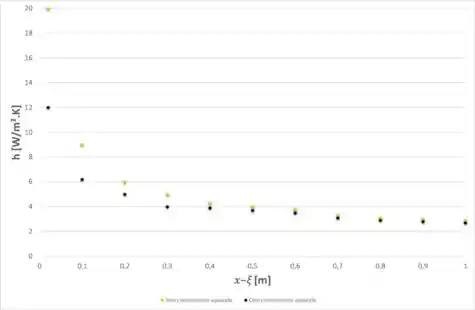
Agora, para a letra (c), precisamos representar o coeficiente convectivo local ao longo da placa para os dois casos, as equações para isso já foram escritas nos passos 4 e 5. Então, para o caso onde não temos o comprimento inicial sem aquecimento, a equação será:
E, para o caso onde temos comprimento inicial sem aquecimento, a equação será:
Então, plotando essas duas funções em um gráfico, tomando o cuidado de utilizar no eixo x a diferença , para poder comparar as duas partes de uma maneira que fique mais visual no gráfico. Ou seja, quando não tivermos comprimento inicial sem aquecimento, termos , e no caso com comprimento inicial sem aquecimento, iremos mostrar a parcela que começa com x = 1 e vai até x = 2. Dessa forma, teremos:
