Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 6.Problemas - Ex. 51

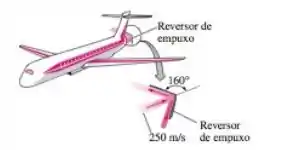
Considere um avião com um motor a jato anexado à seção da cauda que expele gases de combustão a uma taxa de 18   k g / s com velocidade de V = 250   m / s com relação ao avião. Durante a aterrisagem, um reversor de empuxo (que serve como freio para o avião e facilita a aterrisagem em uma pista curta) é abaixado na trajetória do jato de exaustão, o qual deflete a exaustão traseira de 160 ° . Determine ( a ) o empuxo (força para a frente) que o motor produz antes da inserção do reversor de empuxo e ( b ) a força de frenagem produzida após o reversor de empuxo ser empregado.

Passo 1

Fala aí galera, vamos para mais uma questão de Mecânica dos Fluidos. Primeiramente, o empuxo exercido em um avião é simplesmente o fluxo de momento dos gases de combustão na direção reversa, temos:

E = m ˙ V = 18 k g s 250 m s 1   N 1 k g ∙ m s 2 E = 4500   N

Passo 2

Agora, tomamos o inversor de empuxo como o volume de controle, de modo que ele atravesse os fluxos de escape normalmente e as barras de conexão do avião, e a direção do avião como a direção positiva do eixo x . A equação do momento para o escoamento unidimensional constante na direção x reduz para:

∑ F → = ∑ s a í d a β m ˙ V → -   ∑ e n t r a d a β m ˙ V → F R x = m V cos ⁡ 20 ° - m - V ˙ F R x = 1 + cos ⁡ 20 ° m ˙ V i

Substituindo, a força da reação é determinada por:

F R x = 1 + cos ⁡ 20 ° 18 k g s 250 m s F R x = 8729   N

Logo, podemos concluir que a força de frenagem que atua no plano é oposta a F R x , portanto:

F f r e n a g e m = 8729   N

Resposta

E = 4500   N

F f r e n a g e m = 8729   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

o carrinho da Figura P3.107 move-se à velocidade constante V 0 = 12m / s e coleta água com uma concha de 90 cm de largura que se aprofunda h = 2,5c m em um lago. Despreze o arrasto do ar e o atrito da
Modifique o Exemplo 3.15, de modo que o braço parta do repouso e acelere até sua velocidade final de rotação. O momento de inércia do braço em relação a O é I o . Desprezando o arrasto do ar, encontre
Aplique o Problema P3.108 ao seguinte caso: M t o t a l = 900k g , b = 60c m ,h = 2c m ,V o = 120m / s , com o foguete do Problema P3.35 ligado e funcionando. Calcule V após 3 s.
A junta em Y da Figura P3.112 divide a vazão no tubo em partes iguais Q/2, que saem à distância R 0 do eixo, como mostra a figura. Despreze a gravidade e o atrito. Encontre uma expressão para o torque
Um foguete é ligado a uma barra rígida horizontal, articulada na origem, como na Figura P3.104. Sua massa inicial é M 0 e suas propriedades de saída são m ˙ e V s , relativas ao foguete. Estabeleça a