Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 112

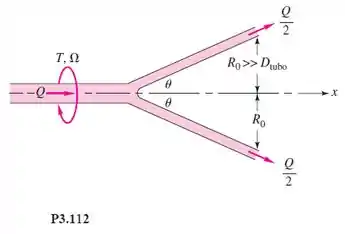
A junta em Y da Figura P3.112 divide a vazão no tubo em partes iguais Q/2, que saem à distância R 0   do eixo, como mostra a figura. Despreze a gravidade e o atrito. Encontre uma expressão para o torque T em torno do eixo x necessário para manter o sistema girando à velocidade angular Ω .

Passo 1

Bora lá resolver mais essa!

Primeiramente, vamos considerar o eixo y em sentido “pra cima”, assim, vamos conseguir encontrar as velocidades absolutas de saída, repare que, como temos uma certa angulação, teremos componente com cosseno e seno, logo:

V p r a c i m a = V 0 cos ⁡ θ i ^ + V 0 sen ⁡ θ j ^ + R 0 Ω   k ^

V p r a b a i x o = V 0 cos ⁡ θ i ^ - V 0 sen ⁡ θ j ^ - R o Ω   k ^

Temos que, V 0 = Q / A , como Q = Q 2 → V 0 = Q / 2 A é a velocidade relativa em cada tubo.

Passo 2

Realizando uma análise de momento veremos que o momento em x está relacionado ao momento angular dos fluxos, assim:

∑ M = T   i ^ = ρ Q 2 R O   j ^ × V p r a c i m a + ρ Q 2 - R 0   j ^ × V p r a b a i x o - ρ Q ( r e n t r a d a V e n t r a d a )

= ρ Q 2 R 0 2 Ω   i ^ - R 0 V 0 Ω   k ^ + ρ Q 2 R 0 2 Ω   i ^ + R 0 V 0 Ω   k ^ - ρ Q 0

Cada braço vai contribuir para o torque através da velocidade angular relativa, então os termos com velocidade linear, vão ser cancelados, chegaremos então em:

T = ρ Q R 0 2 Ω = m ˙ R 0 2 Ω

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um barco a jato capta água através de aberturas laterais e a ejeta por meio de um bocal de diâmetro D∞75m m ; a velocidade do jato é V j . O arrasto sobre o barco é dado por F a r r a s t o = k V 2 ,
O prato circular, cuja seção reta é mostrada, tem um diâmetro externo de 0,20m . Um jato de água, com velocidade de 35m / s , atinge o prato concentricamente. O diâmetro do jato saindo do bocal é 20m
Um jato contínuo de água é empregado para propelir um carrinho ao longo de uma pista horizontal, conforme mostrado. A resistência total ao movimento do carrinho é dada por F D = k u 2 , com k = 0,92N
Água, proveniente de um bocal estacionário, atinge uma pá fixa sobre um carrinho. O ângulo da pá é θ = 120 ° . O carrinho afasta-se do bocal com velocidade constante u = 10m / s à medida que a pá rece
Um jato de óleo ( S G = 0,8 ) atinge uma lâmina curva que desvia o fluido de um ângulo θ = 180 ° . A área do jato é 1200m m 2 e sua velocidade relativa ao bocal estacionário é de 20m / s . Determine a