Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 104
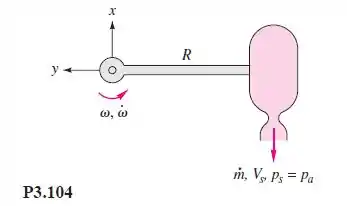
Um foguete é ligado a uma barra rígida horizontal, articulada na origem, como na Figura P3.104. Sua massa inicial é e suas propriedades de saída são e , relativas ao foguete. Estabeleça a equação diferencial do movimento do foguete e a resolva para determinar a velocidade angular da barra. Despreze a gravidade, o arrasto do ar e a massa da barra.
Passo 1
Bora lá resolver mais uma!
O braço tem um tamanho R, certo? Assim, ele fará um movimento circular. Nosso foguete sempre estará tangenciando essa “órbita”, assim, vamos fazer uma análise de quantidade de movimento, logo:
Teremos que:
em que, . A massa irá diminuir de acordo com que o combustível acabe.
Para resolver essa equação, basta integrar tendo quanto . Logo,
Resposta
Exercícios de Livros Relacionados
O prato circular, cuja seção transversal é mostrada, tem um diâmetro externo de 0,15m . Um jato de água o atinge concentricamente e em seguida escoa para fora ao longo da superfície do prato. A veloci
O carrinho mostrado rola com resistência desprezível. Ele deve acelerar para a direita a uma taxa constante de 2,5m / s 2 . Isso deverá ser realizado pela “programação” da velocidade do jato de água,
Considere uma pá defletora simples, com curvatura θ , movendo-se horizontalmente com velocidade constante, u , sob a ação de um jato impingente como no Problema 4.128. A velocidade absoluta do jato é
A catapulta hidráulica do Problema 4,138 é acelerada por um jato de água que atinge sua pá curva e se move ao longo de uma pista horizontal com resistência desprezível. Em um dado instante, sua veloci
A aceleração do conjunto carrinho/pá do Problema 4,128 deve ser controlada pela variação do ângulo da sua pá, θ , a partir do instante em que ele inicia o movimento. Uma aceleração constante, a = 1,5m