Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 9.Problemas - Ex. 58

Considere o bocal da mangueira de jardim do Problema 9-33. Encontre uma expressão para a função corrente correspondendo a esse campo de escoamento.

Passo 1

Primeiramente vamos retomar as informações passadas na questão 9-33.

Temos o seguinte escoamento:

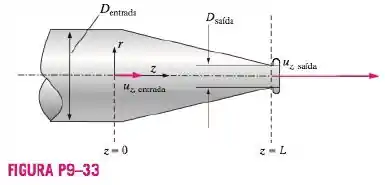
Como é mostrado na figura temos a componente axial da velocidade é representada por u z ,   e n t r a d a e u z ,   s a í d a . Entre z = 0   a z = L ,a componente é dada por:

u z = u z ,   e n t r a d a + u z ,   s a í d a - u z ,   e n t r a d a L ∙ z

Temos também da resolução da questão 9-33 as componentes de velocidade r :

u r = - r 2 ∙ u z ,   s a í d a - u z ,   e n t r a d a L

Assumindo que o fluxo é constante, incompressível e uma função apenas de r e z .

Com estes termos em mente podemos prosseguir para determinar a função de corrente.

Passo 2

Para determinar a função de corrente para este escoamento, podemos utilizar definição dela:

u r = - 1 r ∙ ∂ ψ ∂ z                               u z = 1 r ∙ ∂ ψ ∂ r  

Utilizando uma das coordenadas para determinara a função de corrente ψ , escolherei u z :

u z = 1 r ∙ ∂ ψ ∂ r

Isolando ψ :

r ∙ u z ∙ d r = d ψ

d ψ = r ∙ u z ∙ d r

Integrando dos dois lados, para termos apenas o termo ψ :

∫ d ψ = ∫ r ∙ u z ∙ d r

Substituindo a variável u z :

ψ = ∫ r ∙ u z ,   e n t r a d a + u z ,   s a í d a - u z ,   e n t r a d a L ∙ z ∙ d r

ψ = r 2 2 ∙ u z ,   e n t r a d a + u z ,   s a í d a - u z ,   e n t r a d a L ∙ z + c

Após executarmos uma integral não definida, por via de regra, temos uma constante.

Caso você desejar, verificar a repostas, você pode fazer os mesmo passos com a outra componente u r ,o resultado será o mesmo.

Resposta

ψ = r 2 2 ∙ u z ,   e n t r a d a + u z ,   s a í d a - u z ,   e n t r a d a L ∙ z + c

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Modifique o Problema 8.52 como se segue. Para os mesmos dados do veleiro, encontre a velocidade do vento, em km/h, que irá mover o barco a uma velocidade ótima de 4,1 m/s paralela à quilha.
Uma proposta de velocímetro de corrente livre usaria um cilindro com tomadas de pressão em θ = 180 ° e θ = 150 ° . A diferença de pressão daria uma medida de velocidade da corrente livre U ∞ . Contudo
Em princípio, é possível usar cilindros rotativos como asas de avião. Considere um cilindro de 30 cm de diâmetro, girando a 2400 rpm. Ele deve sustentar um avião de 55 kN voando a 100 m/s. Qual deveri
Considere que o barco a rotor Flettner da figura P8.54 tenha um coeficiente de resistência na água de 0,005. Com que rapidez o barco irá navegar na água do mar a 20°C sob um vento de 6,1 m/s se a quil
O barco a rotor Flettner original tinha aproximadamente 30,5 m de comprimento, deslocava 800 toneladas e tinha uma área molhada de 325 m². Conforme se esboça na figura P8.54, ele tinha dois rotores de