Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 53
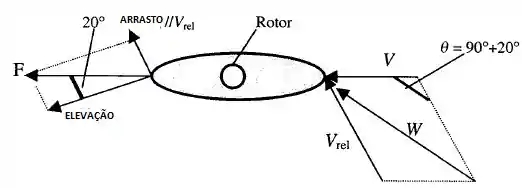
Modifique o Problema 8.52 como se segue. Para os mesmos dados do veleiro, encontre a velocidade do vento, em km/h, que irá mover o barco a uma velocidade ótima de 4,1 m/s paralela à quilha.
Passo 1
E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)! Primeiro passo é DESENHAR!!!
Recuperando os dados da questão P8.52, temos que:
A geometria é a mesma, então mantemos nossa velocidade relativa, ou seja, .
Passo 2
A lei dos cossenos continua válida para aplicação ao nosso sistema!!
Resposta
Exercícios de Livros Relacionados
5.36 Em um escoamento unidimensional e paralelo na direção positiva de x , a velocidade varia lineramente de zero em y = 0 até 30m / s em y = 1,5m . Determine uma expressão para a função de corrente,
Mostre por expansão e separando os termos real e imaginário que f = z 6 (em que z é o número complexo z = x + i y ) conduz a um potencial de velocidade válido (a parte real de f ) e a uma função de co
Considere o escoamento em torno de um cilindro circular com velocidade de corrente livre da direita para a esquerda e um vórtice livre de sentido antihorário. Mostre que a força de sustentação sobre
Um modelo grosseiro de um tornado é formado pela combinação de um sorvedouro, de intensidade q = 2800m 2 / s , e um vórtice livre, de intensidade K = 5600m 2 / s . Obtenha a função de corrente e o pot
Considere o escoamento sobre um cilindro circular de raio a , como no Exemplo 6.11. Mostre que V r = 0 ao longo das linhas ( r , θ ) = r , ± π 2 . Trace um gráfico de V θ U versus o raio para r ≤ a ,