Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 54

O barco a rotor Flettner original tinha aproximadamente 30,5 m de comprimento, deslocava 800 toneladas e tinha uma área molhada de 325 m². Conforme se esboça na figura P8.54, ele tinha dois rotores de 15,2 m de altura e 2,75 m de diâmetro, girando a 750 rpm, o que está bem fora dos limites da figura 8.15. Os coeficientes de sustentação e arrasto medidos para cada rotor ficaram em torno de 10 e 4, respectivamente. Se o barco estivesse ancorado e sujeito a um vento transversal de 7,6 m/s, como na figura P8.54, qual seria a força do vento paralela e normal à linha de centro do barco? Avalie a potência necessária para acionar os rotores.

Passo 1

E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)! Primeiro passo é DESENHAR!!!

Se liga como seria mais ou menos a ideia do problema!!!

A nível do mar, a densidade e viscosidade do ar são:

ρ = 1,225   k g / m ³

μ = 1,78   x   10 - 5   k g / ( m . s )  

Passo 2

Vamos agora colocar as forças que estão atuando no nosso barquinho hehe

F s u s t e n t a ç ã o = C L ρ 2   U ∞ 2 D L

F s u s t e n t a ç ã o = 10 1,225 2 7,6 2 2,75 15,2 x   2   r o t o r e s = 29803,08   N   p a r a l e l o

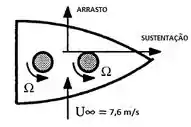
Então a força de arrasto deve ser igual a força de sustentação, certo?

F a r r a s t o = F s u s t e n t a ç ã o

F a r r a s t o = C D C L F s u s t e n t a ç ã o = 4 10 F s u s t e n t a ç ã o = 12010,2   N   ( n o r m a l )

Passo 3

Nós não temos nenhuma fórmula no livro para toque (viscoso) de um cilindro rotativo. Mas uma boa aproximação é assumir que o cilindro simula uma placa plana de tamanho L = 2 π R = 2 π 2,75 2 = 8,6   m . Então, nossa tensão de cisalhamento na parede é:

τ p = C f ρ 2   U 2 = 0,027 R e L 1 7 ρ 2   Ω R 2

Lembre-se que estamos analisando a física na parede, então esse U que está aí na fórmula não é mais a velocidade do vento, mas a velocidade em m/s de rotação do cilindro, beleza?

Ω R = 750 2 π 60 2,75 2 = 108   m / s

Além disso, temos que:

R e L = ρ U L μ = 1,225 108 8,6 1,75   x   10 - 8 = 6,5   x   10 7

Substituindo então os valores na equação da tensão de cisalhamento, encontramos que:

τ p = 14   P a

Portanto, o torque exercido será dado por:

T = τ p π D L R = 14 π 2,75 15,2 2,75 2 = 2528   J

Passo 4

A potência total então é dada como sendo:

P o t = T Ω = 2528 750   x 2 π 60 = 198540   W

Só que isso é para um rotor, precisamos de dois, então temos:

P o t t o t a l = 397079   W

Resposta

F s u s t e n t a ç ã o p a r a l e l a = 29803,08   N  

F s u s t e n t a ç ã o n o r m a l = 12010,2   N  

τ p = 14   P a

P o t t o t a l = 397   k W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As partículas de um fluido movem-se no plano x y com trajetórias definidas por x = x 0 + t ; y = y 0 + t 2 .Obter a equação e desenhar a trajetória da partícula que, no instante t=0, encontra-se em P
Dado o escoamento cujo campo de velocidades é: v x = x t ; v y = y t ; v z = 0 , determinarA equação da linha de corrente que passa pelo ponto P 1 2 ; 1 ; 2 A equação da trajetória que passa por P 1 ,
Dada a função de corrente Ψ = a r - b θ , para r ≠ 0 , onde a e b são constantes positivas:Determinar a equação das trajetórias;Calcular a vazão em volume através de uma superfície semicircular de rai
Dada a função potencial ϕ = x 2 - y 2 para um fluido incompressível em movimento plano irrotacional, determinara função potecialo campo de velocidades
Dado o campo de velocidades do escoamento plano de um fluido ideal incompressível: v x = 2 x 2 2 - t - 6 x ⋅ f y , t ⋅ ln ⁡ t v y = - 6 x 2 y2 - t + 2 y 3 ( 2 - t ) Determinar f ( y , t ) para que o e