Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 8.Problemas - Ex. 55

Considere que o barco a rotor Flettner da figura P8.54 tenha um coeficiente de resistência na água de 0,005. Com que rapidez o barco irá navegar na água do mar a 20°C sob um vento de 6,1 m/s se a quilha se alinha por si mesma com a força resultante sobre os rotores? Dica: Este é um problema com velocidades relativas.

Passo 1

E aí, gente!! Tudo bem? Então vou mostrar pra vocês que mecânica dos fluidos não é nem de longe um bicho de 7 cabeças (nem de perto também)!!

Vamos primeiro pegar as propriedades do ar e da água do mar, beleza?

ρ a r = 1,225   k g / m ³

ρ m a r = 0,00386   k g / m ³

μ = 0,001   k g / ( m . s )

Do problema P8.54, temos as dimensões dos rotores como 2,75 m de diâmetro e 15,2 m de altura. Além disso eles giram com velocidade angular de Ω = 750   r p m . Também tivemos do problema citado os coeficientes de arrasto e sustentação como sendo, C D = 4 e C L = 10 .

Passo 2

Vamos fazer um esquema pra entender o que está acontecendo, beleza?

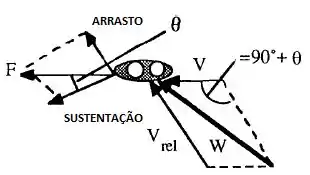
Pelo esquema acima, o arrasto e a sustentação combinam-se na quina do navio. Então θ = tan - 1 ⁡ 4 10 = 21,8   °

Portanto o ângulo entre V e V r e l é igual a 90° + θ , ou seja, temos um ângulo de 90+21,8 = 111,8°.

Onde V e W é a velocidade do navio e do vento, respectivamente.

Passo 3

Temos que o impulso gerado será dado pela força F e que ele deve ser igual a nossa força de arrasto, certo?

F = C L 2 + C D 2 1 2 ρ a r 2 V r e l 2 D L   2 = F a r r a s t o = C D   ρ á g u a 2 V 2 A m o l h a d a

Esse fator “2” em destaque é porque vamos calcular essa força total que atua nos DOIS ROTORES!!

Note que área molhada foi dada também no problema anterior, que é de 325 m².

F = 10 2 + 4 2 1 2 1,225 2 V r e l 2 2,75 15,2 2 = 0,005 998 2 V 2 ( 325 )

V r e l = 1,23 V

Passo 4

Podemos aplicar aqui a leis dos cossenos, certo?

W 2 = V 2 + V r e l 2 - 2 V V r e l c o s ⁡ ( θ + 90 )

6,1 2 = V 2 + 1,23 V 2 - 2 V 1,23 V cos ⁡ 118 → V b a r c o = 3,3   m / s

Resposta

V b a r c o = 3,3   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

É dada a função de corrente Ψ = x 2 + 2 x y + 4 t 2 y . No instante t = 2s , determinarQual é a vazão por unidade de espessura entre (A) e (B)Qual é a vazão por unidade de espessura entre (A) e (C)
No estudo analítico de um furacão, admitiu-se que o escoamento resulte da superposição de um vórtice ideal com um sorvedouro no ponto O. Sendo a função potencial do sorvedouro ϕ = - q 2 π ln ⁡ r e a f
Seja um meteorito que penetra na atmosfera. Admitir em primeira aproximação que o escoamento seja bidimensional e irrotacional na região próxima ao ponto de estagnação. Sabe-se que o escoamento pode s
Dado o campo de velocidades v → P , t = 6 x ⋅ e → x + 6 y ⋅ e → y + 7 t ⋅ e → z , determinarA velocidade e a aceleração no ponto ( 3 ; 2 ;z ) , no instante t = 1 As linhas de corrente no instante t =
A função de corrente de um escoamento plano de um fluido incompressível, entre duas placas infinitas, paralelas é dada por: Ψ = v 0 2 L y 2 Determinar o diagrama de velocidades e representa-lo grafica