Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 11.Problemas - Ex. 57

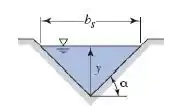
Considere um canal aberto simétrico de seção transversal triangular. Mostre que para uma dada área de escoamento, o perímetro molhado é minimizado quando os lados se encontram em um ângulo reto.

Passo 1

Tá legal, então, para mostrar que o perímetro molhado é minimizado quando os lados se encontram em um ângulo reto, primeiro vamos precisar da equação do perímetro molhado, e depois, como eles se encontram em um ângulo reto, o valor de α no esquema do enunciado deve ser 45°. Dessa forma com o auxílio da tabela de geometria fornecida nessa seção, temos:

A = y 2 c o t g   α

P = 2 y s e n   α

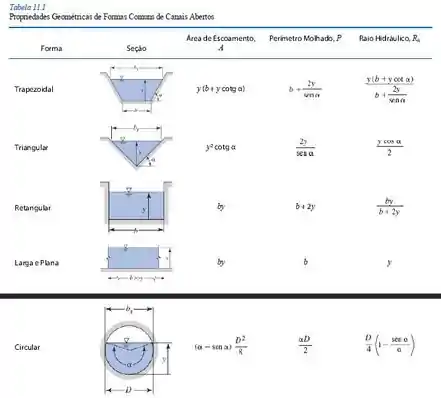
Passo 2

Então agora, vamos isolar y da equação da área e substituir na do perímetro, então, temos:

A = y 2 c o t g   α → y = A c o t g   α

Substituindo essa expressão na equação do perímetro molhado, temos:

P = 2 y s e n   α = 2 s e n   α A c o t g   α → P = 2 s e n   α A t g   α

Jogando o termo s e n   α para dentro da raiz, temos:

P = 2 A s e n   α s e n 2 α ( cos ⁡ α ) → P = 2 A s e n   α ( cos ⁡ α )  

Passo 3

Então, para minimizar o perímetro, podemos derivar a equação encontrada no passo 2 com relação à α (lembrando que aqui precisamos usar a regra do produto e do quociente) e igualar ela a zero, então, temos:

d P d α = 2 0 s e n   α cos ⁡ α - A cos ⁡ α cos ⁡ α + s e n   α - s e n   α s e n   α cos ⁡ α 2 = 2 A s e n 2 α - A c o s 2 α s e n 2 α cos 2 ⁡ α

Igualando essa expressão a zero, temos:

2 A s e n 2 α - A c o s 2 α s e n 2 α cos 2 ⁡ α = 0 → A s e n 2 α - A c o s 2 α = 0 → s e n 2 α = cos 2 ⁡ α

Da relação fundamental, sabemos que s e n 2 α = 1 - cos 2 ⁡ α , então, a equação se torna:

1 - cos 2 ⁡ α = cos 2 ⁡ α → 1 = 2 cos 2 ⁡ α → cos ⁡ α = 1 2 → α = 45 °

Pronto! Chegamos no valor que precisávamos para a demonstração.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Água escoa em um canal trapezoidal a uma profundidade normal de 1,2 m. A largura do fundo é de 2,4 m e a inclinação lateral é de 1:1 ( 45 ° ). A vazão é 7,1 m 3 s . O canal é escavado na terra nua. De
Um canal retangular com 2 m de largura e inclinação de 0,0005 possui uma profundidade de escoamento de 1,5 m. O coeficiente de rugosidade de Manning é de 0,015. Determine a descarga uniforme em regime
Um canal com seção transversal quadrada deve carregar 20 m3/s de água a uma profundidade normal sobre uma inclinação de 0,003. Compare as dimensões do canal requerido para (a) concreto e (b) argamassa
Determine a profundidade de escoamento uniforme em um canal retangular com 2,5 m de largura com uma descarga de 3 m 3 s . A inclinação é 0,0004 e o fator de rugosidade de Manning é de 0,015.
Determine a profundidade de escoamento uniforme em um canal trapezoidal com largura no fundo igual a 2,5 m e inclinações laterais de 1 na vertical para 2 na horizontal com uma descarga de 3 m 3 s . A