Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 114
A maior turbina eólica Darrieus conhecida, de eixo vertical, foi construída pelo DOE (Departamento de Energia dos Estados Unidos) perto de Sandia, no Novo México [48]. Essa máquina tem altura de 18 m e raio de 5 m; a área varrida pelo rotor é por volta de 110 m². Se o rotor for constrangido a rodar a 70 rpm, trace a potência em kW que esta turbina eólica pode produzir para velocidades do vento entre 2,57 m/s e 25,7 m/s.
Passo 1
Tá legal, a primeira coisa que devemos fazer é analisar o diagrama do coeficiente de potência fornecido nessa seção:
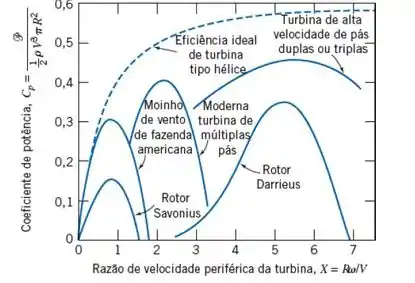
Então, nesse caso, como temos um rotor Darrieus, vamos assumir a condição de máxima potência, de forma que:
E, para esse valor de coeficiente de potência, temos:
Então, nessa condição, a velocidade do vento será:
E, a velocidade periférica do rotor será:
Passo 2
Da equação do coeficiente de potência, temos:
No entanto, o valor de representa a seção do rotor, que nesse caso já foi fornecida no enunciado, então temos , substituindo esse valor na expressão anterior, temos:
E, substituindo os valores conhecidos, chegamos em:
Passo 3
Então, plotando o gráfico da função encontrada no passo 2 para o intervalo de interesse pedido no enunciado, lembrando de calcular para toda velocidade em questão através do valor de a partir do gráfico do passo 1, temos:
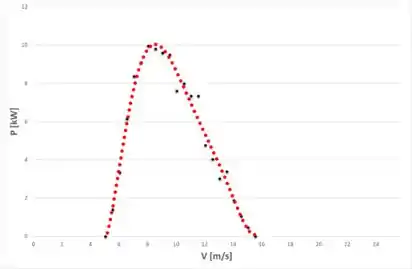
Podemos observar que para os valores de velocidade do vento menores que 4,5 m/s e maiores que 16 m/s não temos potência, pois para essas velocidades temos e por consequência .
Resposta
Ei, a resposta está no passo a passo :)