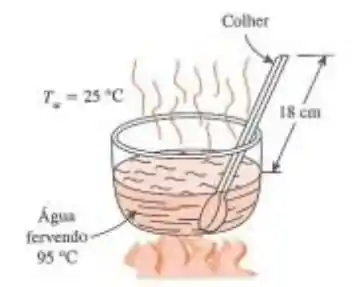
Considere uma colher de aço inoxidável parcialmente imersa em água em ebulição a 95°C, em uma cozinha a 25°C. O cabo da colher possui uma seção transversal de e se estende 18 cm no ar livre a partir da superfície da água. Considerando que o coeficiente de transferência de calor nas superfícies expostas do cabo da colher é de , determine a diferença de temperatura através da superfície exposta do cabo da colher. Declare suas suposições.

Bora começar mais umaaa !!

O que nós queremos aqui é a diferença de temperatura entre a parte imersa da colher e parte superior do cabo, exposta ao ar.

A parte superior do cabo está localizada à uma distância L da parte imersa e, por isso, vamos chama-la de T(x).

Sendo assim, o que queremos é:

Já sabemos que a parte imersa terá a mesma temperatura da água em ebulição:

Agora nós vamos assumir que o processo seja adiabático, então a temperatura pode ser dada pela fórmula:

Como queremos a temperatura na ponta:

Então:

Já temos que:

Mas falta achar o m, certo?

Se lembrarmos que ele é dado por:

Para uma superfície considerada retangular:

O problema nos diz que o cabo da colher tem área , então podemos assumir que:

Se é assim:

E:

Achando m:

Na fórmula da temperatura: