Considere o disco opaco, cinza e difuso,, que tem um diâmetro de , uma emissividade de e se encontra a uma temperatura de . Coaxialmente ao disco , existe um disco negro em forma de anel, , que se encontra a e apresenta as dimensões mostradas na figura. A parte posterior de é isolada e não irradia diretamente o disco detector, , resfriado criogenicamente. Esse disco tem diâmetro de e está localizado a de distância de .

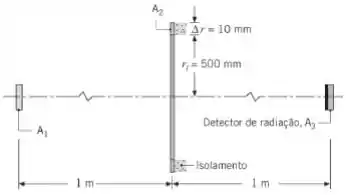
Calcule a taxa na qual a radiação incide sobre devido à emissão e à reflexão a partir de .

Para resolver essa questão vamos assumir:

(1) é cinza difuso;

(2) é preto;

(3) e a distância de separação;

(4) , de modo que ;

(5) Parte traseira de seja isolada.

A potência radiante que deixa interceptada por tem a forma,

Onde para esta configuração de e ,

Então,

E,

A irradiação em devido à emissão de , vai ter a seguinte carinha:

Onde,

É constante sobre a superfície e da geometria,

E,

Então,

Usando,

E,

Então o poder radiante é,

Com isso fechamos nossa questão! 😊