Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 92

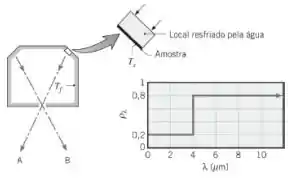
Um equipamento normalmente usado para medir a refletividade de materiais é mostrado na figura. Uma amostra resfriada por água, com 30   m m de diâmetro e temperatura T s   =   300   K , é fixada junto à superfície interior de um grande compartimento fechado. As paredes do compartimento são cinzas e difusas, com uma emissividade de 0,8 e uma temperatura uniforme T f   =   1000   K . Uma pequena abertura localizada na parte inferior do compartimento permite a visão da amostra ou da parede do compartimento. A refletividade espectral ρ λ de uma amostra de um material opaco e difuso é mostrada na figura. O coeficiente de transferência de calor por convecção entre a amostra e o ar no interior da cavidade, que também está a 1000   K , é h   =   10   W / ( m 2 · K ) .

(a) Calcule a absortividade da amostra.

(b) Calcule a emissividade da amostra.

(c) Determine a taxa de remoção de calor ( W ) pelo refrigerante.

(d) A razão entre a radiação na direção A e a radiação na direção B irá fornecer a refletividade da amostra. Explique sucintamente o por quê.

Passo 1

Bora ver o que temos nessa questãozitcha? Aqui nos é dado que uma pequena amostra de refletividade, ρ λ e diâmetro, D , é irradiada com um invólucro isotérmico em T f .

Com isso queremos encontrar a absorptividade, α , da amostra com ρ λ , a emissividade, ε , da amostra e o calor removido pelo refrigerante para a amostra. Além disso, temos que dar uma explicação do motivo pelo qual o sistema fornece a medida de ρ λ . Vamos lá!

Passo 2

Para resolver essa questão vamos assumir que:

(1) A amostra é difusa e opaca;

(2) O forno é um compartimento isotérmico com área muito maior que a amostra;

(3) A abertura do forno é pequena.

Bom, primeiro vamos encontrar a absortividade,   α , onde a irradiação na amostra é:

G   =   E b   T f               e                   α λ   =   1   -   ρ λ

Então,

α = ∫ 0 ∞ α λ G λ d λ G = ∫ 0 ∞ 1 - ρ λ E λ , b λ , 1000 K d λ E b 1000 K

α = 1 - ρ λ F ( 0 → λ 1 ) + 1 - ρ λ , 2 1 - F 0 → λ 1

Usando a tabela 12.1 para λ 1 T f = 4 × 1000 = 4000 μ m . K ,

F 0 - λ = 0,481

Substituindo na expressão de α ,

α = 1 - 0,2 × 0,481 + 1 - 0,8 × 1 - 0,481 = 0,49

Passo 3

A emissividade, ε , segue a Tabela 12.1 com ε λ   =   α λ   =   1   -   ρ λ , pois a amostra é difusa. Então,

ε = E T s E b T s = ∫ 0 ∞ ε λ E λ , b λ , 3 00 K d λ E b 3 00 K

ε = 1 - ρ λ , 1 F ( 0 → λ 1 ) + 1 - ρ λ , 2 1 - F 0 → λ 1

Usando a Tabela 12.1 para λ 1   T s   =   4   ×   300   =   1200   μ m ⋅ K ,  

F ( 0 - λ )   =   0,002

Substituindo na expressão de ε ,

ε = 1 - 0,2 × 0 , 002 + 1 - 0,8 × 1 - 0 , 002 = 0 , 20

Passo 4

Realizando um balanço de energia na amostra, a taxa de remoção de calor pela água de resfriamento é,

q r e s f = A s [ α G + q c o n v ' ' - ε E b T s ]

Onde,

G = E b T f = E b ( 1000 K )

q ’ ’ c o n v = h T f - T s

A s = π D 2 4

Substituindo os valores,

q r e s f = π 4 0,03 m 2 [ 0,49 × 5,67 × 10 - 8 W m 2 . K 4 10 00   K 4 + 10 W m 2 . K 1000 - 300 K - 0,20 × 5,67 × 10 - 8 W m 2 . K 4 3 00   K 4 = 24,5   W

Passo 5

Para responder a (d) vamos supor que a reflexão faça a contribuição dominante para a radiosidade da amostra. Ao visualizar na direção A, a potência radiante espectral é proporcional a ρ λ   G λ .

Na direção B, a potência radiante espectral é proporcional a   E λ ,   b   ( T f ) . Observando que G λ   =   E λ ,   b   ( T f ) , a razão fornece ρ λ .

Apesar da questão ter o enunciado grande, sua resolução não foi tão grande assim, por agora é só 😉

Resposta

  1. α = 0,49
  2. ε = 0,20
  3. q r e s f = 24,5   W
  4. Ao visualizar na direção A, a potência radiante espectral é proporcional a ρ λ   G λ . Na direção B, a potência radiante espectral é proporcional a   E λ ,   b   ( T f ) . Observando que G λ   =   E λ ,   b   ( T f ) , a razão fornece ρ λ .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um forno tem forma cilíndrica com R = H = 3m . As superfícies de base, do topo e dos lados do forno são todas negras e mantidas a uma temperatura uniforme de 500 , 700 e 1.400K , respctivamente. Deter
Uma sala 2,75m de altura, com uma superfície de base de 3,7m × 3,7m devem ser aquecida por aquecedores de resistência elétrica colocados no teto, mantendo a temperatura uniforme de 32° C em todos os m
Considere uma superfície quente cilíndrica e um disco orientado como mostrado abaixo. A superfície cilíndrica e o disco comportam-se como um corpo negro. O cilindro tem diâmetro D e comprimento L de 0
O que é superfície rerradiante? Quais simplificações a superfície rerradiante oferece na análise da radiação?
O que são resistências à radiação de superfície e de espaço? Como são expressas? Para quais tipos de superfícies a resistência à radiação de superfície é zero?