Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 46

Considere um escoamento na camada limite laminar para estimar o arrasto sobre as quatro placas quadradas (cada uma com dimensões de 7,5   c m   x 7,5   c m ) colocadas paralelas a um escoamento de água a 1   m / s , para as duas configurações mostradas. Antes de calcular, que configuração você esperaria experimentar o menor arrasto? Considere que as placas conectadas por um cordão estão suficientemente distantes umas das outras para tornar desprezíveis os efeitos de esteira, também que a água está a 20   ° C .

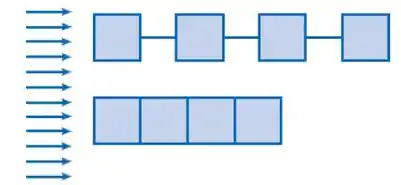
Passo 1

O enunciado diz que o escoamento é laminar, e pede para calcularmos a força de arrasto. Como ele é laminar em placa plana, valem as relações:

c f = 0,730 R e x ,     c f = τ w 1 2 ρ U 2

Ele também dá ums informações importantes:

Velocidade de corrente livre: U = 1   m / s

Água a 20 ° C ,   o que implica em ρ = 998   k g / m 3 e μ = 1 , 01 ⋅ 10 - 3 N ⋅ s / m

Temos duas situações: uma em que as quatro placas estão juntas, logo:

b = 0,075   m ,   L = 0,3 m

E outra quando elas estão separadas, aí a gente pode considerar que são quatro placas com:

b = 0,075   m ,   L = 0,075   m

Ele quer saber em que situação a força de arrasto é maior. A gente pode esperar que ela seja maior na situação de placas separadas, porque a tensão de cisalhamento é maior na região onde o fluído encontra o começo da placa e depois cai rapidamente. Como nessa situação, esse encontro acontece quatro vezes, a força provavelmente será maior. Mas vamos provar isso aí!

Passo 2

A força total de arrasto pode ser definida como:

F D = ∫ τ w d A

Então precisamos de uma expressão para τ w .

Como a gente encontra isso? Usando as equações da camada limite:

c f = 0,730 R e x ,     c f = τ w 1 2 ρ U 2

0,730 ρ U x μ = τ w 1 2 ρ U 2 ∴ τ w = 0,730 μ U ρ x ⋅ 1 2 ρ U 2 = 0,365 μ ρ U 3 ⋅ x - 1 2

Uhul! Conseguimos!

Passo 3

Agora, começamos a montar a nossa integral:

F D = ∫ τ w d A

Podemos escrever:

d A = b d x

Sabendo que 0 < x < L :

F D = ∫ 0 L 0,365 μ ρ U 3 x ⋅ b d x = 0,365 b μ ρ U 3 ⋅ ∫ 0 L x - 1 2 d x = 0,365 b μ ρ U 3 ⋅ 2 L

Passo 4

Precisamos substituir os dados do problema, para cada situação:

- Placas separadas: A gente vai multiplicar a força de uma por quatro.

b = 0,075   m ,   L = 0 , 075 m

F D = 0 , 730 b μ ρ U 3 L

F D s = 4 ⋅ 0,730 ⋅ 0,075 ⋅ 1,01 ⋅ 10 - 3 ⋅ 998 ⋅ 1 3 ⋅ 0,075 = 6,0 ⋅ 10 - 2 N

Isso se a gente pensar na força em um lado só das placas. Pensando na força aplicada em ambos os lados, é só multiplicar por 2 :

2 F D s = 12 , 0 ⋅ 10 - 2 N

- Placas juntas:

b = 0,075   m ,   L = 0 , 3 m

F D = 0,730 b μ ρ U 3 L

F D J = 0,730 ⋅ 0,075 ⋅ 1,01 ⋅ 10 - 3 ⋅ 998 ⋅ 1 3 ⋅ 0 , 3 = 3,0 ⋅ 10 - 2 N

Isso se a gente pensar na força em um lado só das placas. Pensando na força aplicada em ambos os lados, é só multiplicar por 2 :

2 F D J = 6 , 0 ⋅ 10 - 2 N

Ih a gente estava certo! A força é maior na situação das placas separadas.

Arrasamos! haha

Resposta

2 F D s = 12,0 ⋅ 10 - 2 N

(placas separadas, força maior)

2 F D J = 6,0 ⋅ 10 - 2 N

(placas juntas, força menor)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que você compre uma chapa de madeira compensada e coloque-a sobre o porta-bagagem no teto do seu carro (veja a Figura P7.23). Você se dirige para casa a 56 km/h. (a) Considerando que a chapa e
Com base estritamente no seu conhecimento sobre a teoria da placa plana mais os gradientes de pressão adverso e favorável, explique em que direção (esquerda ou direita) o escoamento de ar em torno do
Uma chapa fina de fibra pesa 90 N e se localiza sobre o topo de um telhado, como mostra a Figura P7.45. Considere ar ambiente a 20°C e 1 atm. Se o coeficiente de atrito sólido entre a chapa e o telhad
Como um caso semelhante ao do Exemplo 7.5, Howarth também propôs a distribuição de velocidades com gradiente adverso U = U 0 ( 1 - x 2 L 2 ) e calculou a separação em x s e pL = 0,271 por um método de
Em 1957, H. Görtler propôs os seguintes casos-teste com gradientes adversos U = U 0 1 + x L η e calculou a separação para escoamento laminar caso η = 1 como x s e p L = 0,159 . Compare com o método de