Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 7.Problemas - Ex. 45
Uma chapa fina de fibra pesa 90 N e se localiza sobre o topo de um telhado, como mostra a Figura P7.45. Considere ar ambiente a 20°C e 1 atm. Se o coeficiente de atrito sólido entre a chapa e o telhado for , que velocidade do vento gerará atrito fluido suficiente para desalojar a chapa?
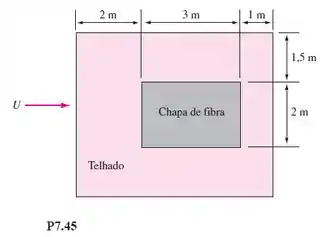
Passo 1
E bora lá pra mais uma!
Temos para o ar que e . Bora assumir um escoamento turbulento, com isso, descobriremos a força de arraste quando a borda não está em x=0, assim:
Igualemos isso a força de deslocamento, dada por , assim:
Resolvendo, teremos
Resposta
Exercícios de Livros Relacionados
Uma placa plana delgada é instalada em um túnel de água como uma divisora de fluxo. A placa tem 0,3m de comprimento e 1m de largura. A velocidade de corrente livre é 1,6m / s . Camadas limite laminare
Considere um escoamento na camada limite laminar para estimar o arrasto sobre a placa plana mostrada quando colocada em um escoamento de ar a 7 , 5m / s , porém considerando que a base da placa está d
Considere um escoamento na camada limite laminar para estimar o arrasto sobre a placa plana mostrada quando colocada em um escoamento de ar a 7 , 5m / s . O ar está a 20 ° C e a 101,3 k P a . (Note qu
Verifique que a componente y da velocidade para a solução de Blasius das equações da camada limite de Prandtl é dada pela Eq. 9.10. Obtenha uma expressão algébrica para a componente x da aceleração de
Considere um escoamento na camada limite laminar para estimar o arrasto sobre as quatro placas quadradas (cada uma com dimensões de 7,5c m x 7,5c m ) colocadas paralelas a um escoamento de água a 1m /