Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 9.Problemas - Ex. 34
Verifique que a componente da velocidade para a solução de Blasius das equações da camada limite de Prandtl é dada pela Eq. 9.10. Obtenha uma expressão algébrica para a componente da aceleração de uma partícula fluída na camda limite laminar. Trace versus para determinar a máxima componente da aceleração para um dado valor de .
Passo 1
A gente pode pensar o enunciado em duas partes: em uma a gente vai precisar provar, a partir das relações de Blasius, que a expressão da componente da velocidade tem essa cara:
Na segunda parte, a gente precisa achar a expressão para , a partir das expressões de Blasius também e depois plotar o gráfico.
Vamos lá?
Passo 2
Podemos lembrar que por Blasius:
Temos também a expressão da função corrente:
A componente da velocidade é definida por:
Temos que calcular essa derivada usando a regra da cadeia para e a regra do produto, pois há duas funções de :
Passo 3
Calculando a derivada de separadamente e jogando alguns termos para dentro da raiz:
Lembrando que:
Voltando a expressão de :
Passo 4
Agora a gente só precisa arrumar esses termos, colocando o que der dentro das raízes:
Por fim,
Ufa! Mas ainda não acabou. Haha
Passo 5
Agora vem a segunda parte. Para ela a gente tem que lembrar da expressão para calcular a aceleração na direção :
E que para gente,
Então, vamos calcular essas duas derivadas parciais. Pela regra da cadeia:
Passo 6
Agora a gente tem a expressão das derivadas, de e . Só substituir:
A gente pode arrumar isso, fazendo aquela paradinha de colocar termos para dentro da raiz, aí fica desse jeito:
Finalmente, colocando alguns termos em evidência:
Passo 7
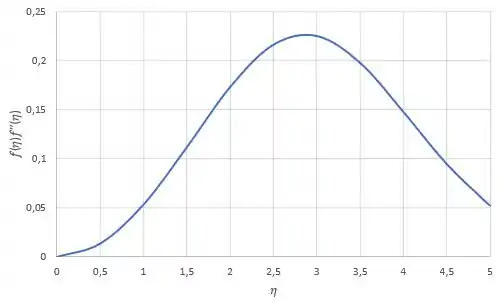
Precisamos plotar o gráfico e achar onde temos a componente máxima em função de . Podemos plotar o gráfico de em função de , para achar o máximo desse termo, achando assim o máximo de , em função de :
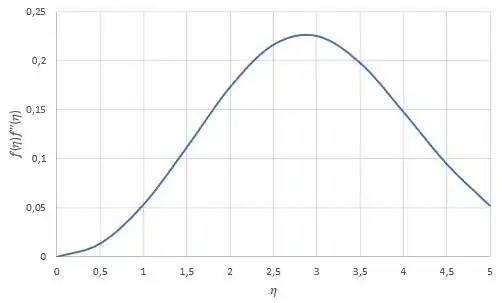
O máximo ocorre em aproximadamente , onde .
Por isso, o valor máximo de é:
Resposta
