Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 12.Problemas - Ex. 93

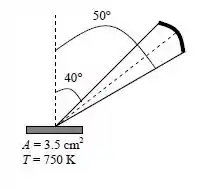
Considere uma pequena superfície negra de área A = 3,5 cm² mantida a 750 K. Determine a taxa em que a energia de radiação é emitida pela superfície através da abertura em forma de anel, definida por 0 ≤ ϕ ≤ 2 π e 40 ° ≤ θ   ≤ 50 ° , onde ϕ é o ângulo de azimute e θ é o ângulo que o feixe de radiação faz com a normal da superfície.

Passo 1

A taxa de emissão de radiação de uma superfície por unidade de área na direção apresentada aí no enunciado é dada pela seguinte equação:

d E = d Q d A = I θ , ϕ cos ⁡ θ s e n θ d θ d ϕ

Passo 2

A taxa total emitida vai ser a integral dessa equação nos intervalos apresentados pra gente no enunciado, ou seja...

E = ∫ 0 2 π ∫ 40 50 I θ , ϕ cos ⁡ θ s e n θ d θ d ϕ = I b 0,1736 π

Note que eu escrevi agora Ib que é para um corpo negro, onde a gente pode escrever assim:

E = σ T 4 π 0,1736   π = 0,1736 σ T 4

Passo 3

Agora vamos substituir essa equação na primeira lá do passo 1 e ser feliz meu povo!!!

Mas vale lembrar que como estamos considerando uma área tão pequena dada pelo enunciada, que podemos dizer que ela é a própria área na forma diferencial, beleza?

q = E d A = 0,1736 σ T 4 d A = 0,1736 5,67 x 10 - 8 750 4 3,5 x 10 - 4 = 1,09   W

Resposta

q = 1,09   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considerando comportamento de corpo negro, determine a temperatura de, e a energia emitida pela, área A 1 no Exemplo 12.1 e nos Problemas 12.8 e 12.14, assim como a área A a no Problema 12.12.
Determine a fração do poder emissivo hemisférico total que deixa uma superfície difusa nas direções π / 4≤θ≤π / 2 e 0≤ϕ≤π .
O fluxo de energia associado à radiação solar que incide sobre a superfície externa da atmosfera terrestre foi medido com precisão e seu valor é de 1368W / m 2 . Os diâmetros do Sol e da Terra são de
Considere uma superfície difusa quadrada Δ A o com 5m m de lado, que tem um poder emissivo total E o=4000W / m 2 . O campo de radiação devido à emissão para o espaço hemisférico acima da superfície é
A superfície escura do topo de um fogão cerâmico pode ser aproximada por um corpo negro. Os “queimadores”, que estão integrados ao topo do fogão, são aquecidos por baixo por aquecedores de resistência