Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 17
Considere uma superfície difusa quadrada com de lado, que tem um poder emissivo total . O campo de radiação devido à emissão para o espaço hemisférico acima da superfície é difuso, proporcionando assim uma intensidade uniforme Além disso, se o espaço for um meio não participante (não absorvedor, não espalhador e não emissor), a intensidade é independente do raio para qualquer direção Assim, as intensidades em quaisquer pontos e seriam iguais.
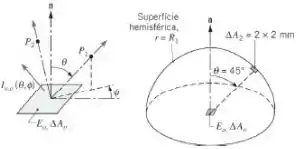
(a) Qual é a taxa na qual a energia radiante é emitida por ?
(b) Qual é a intensidade do campo de radiação emitido a partir da superfície ?
(c) Partindo da Equação 12.13 e presumindo o conhecimento da intensidade , obtenha uma expressão para .
(d) Considere a superfície hemisférica localizada em . Usando a exigência de conservação da energia, determine a taxa na qual a energia radiante incide sobre essa superfície devido à emissão a partir de .
(e) Utilizando a Equação 12.10, determine a taxa na qual a energia radiante que deixa é interceptada por uma pequena área localizada na direção sobre a superfície hemisférica. Qual é a irradiação sobre ?
(f) Repita a parte (e) para a localização Os valores das irradiações nas duas localizações são iguais?
(g) Usando a Equação 12.18, determine a irradiação sobre a superfície hemisférica em .
Passo 1
Oi! Eu sei que essa questão parece ser imensa e assustadora mas cão que ladra não morde, né não? Então fica tranquilo e vem comigo que você vai ver que ela não é tão grande assim 😉.
Aqui nós temos uma superfície difusa , quadrado de , com potência emissiva total E com isso queremos encontrar do campo de radiação emitido a partir da superfície , uma expressão para .
Além da taxa na qual a energia radiante incide sobre a superfície hemisférica devido à emissão a partir de , a taxa na qual a energia radiante que deixa é interceptada por localizada na direção e sobre a superfície hemisférica, a irradiação sobre e
Passo 2
Para resolver essa questão vamos assumir superfície difusa, , meio acima de não participa e A potência radiante que deixa por emissão é,
A intensidade emitida é é independente da direção, já que ΔAo é um emissor difusor,
As intensidades nos pontos e também são e a intensidade permanecerá constante, não importando a que distância o ponto esteja da superfície , uma vez que o espaço não é participativo.
Passo 3
Pelo conhecimento de , a potência radiante saindo de é,
Definindo as superfícies de controle acima de e em , a potência radiante que sai de deve passar por .
A irradiação média no hemisfério, , em que,
Com base na definição,
Onde é o incidente de energia radiante na superfície
Passo 4
A potência radiante que deixa interceptada por , onde , localizada em segue da seguinte expressão:
Onde e o ângulo sólido subtende em relação a é,
Onde , a direção normal para
A partir da definição de irradiação,
Passo 5
Com localizado em , onde encontramos:
Observe que a irradiação em quando está localizada em é maior do que quando está localizado em
Passo 6
Baseado na Figura 12.10, encontramos:
Onde a área elementar na superfície hemisférica e o ângulo sólido subtende em relação a são, respectivamente,
A partir deste cálculo, temos que a irradiação média na superfície do hemisfério,, é
Fim 😊
Resposta
- A irradiação em quando está localizada em é maior do que quando está localizado em