Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 9

Considere os retângulos perpendiculares mostrados na figura.

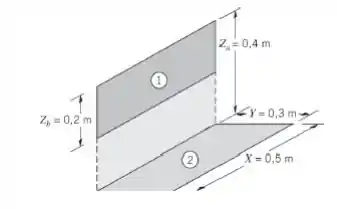
(a) Determine o fator de forma F 12 .

(b) Para larguras dos retângulos de X   =   0,5 ;   1,5 e 5   m , represente graficamente F 12 como uma função Z b para 0,05   ≤   Z b   ≤   0,4   m . Compare os seus resultados com o fator de forma obtido pela relação bidimensional para placas perpendiculares com uma aresta comum (Tabela 13.1).

Passo 1

Heyy, nessa questão aqui nós temos dois retângulos perpendiculares sem borda comum. E a partir disso queremos encontrar o fator de forma, F 12 .

Passo 2

Para resolver essa questão vamos assumir que todas as superfícies são difusas e que o plano formado por A 1   +   A 3   é perpendicular ao plano de A 2 . Apresentando a superfície hipotética A 3 , podemos escrever:

F 2 ( 3,1 ) = F 23 + F 21

Usando a Fig. 13.6, aplicável a retângulos perpendiculares com uma aresta comum, encontramos:

F 23 = 0,19

Com,

Y = 0,3

X = 0,5

Z = Z a - Z b = 0,2

E,

Y X = 0,3 0,5 = 0,6

Z X = 0,2 0,5 = 0,4

Passo 3

E também,

F 2 ( 3 , 1 ) = 0 , 25

Com,

Y = 0,3

X = 0,5

Z = Z a - Z b = 0 , 4

E,

Y X = 0,3 0,5 = 0,6

Z X = 0 , 4 0,5 = 0 , 8

Então,

F 21 = F 2 ( 3,1 ) - F 23 = 0,25 - 0,19 = 0,06

Por reciprocidade,

F 21 = A 2 A 1 F 21 = 0,5 × 0,3   m 2 0,5 × 1,2 m 2 × 0,06 = 0,09

Resposta

F 21 = 0,09

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os fatores de forma F 13eF 2 3 entre as superfícies retangulares mostradas na Fig. P13–8.
Considere um recinto cilíndrico cuja altura é duas vezes o diâmetro de sua base. Determine o fator de forma da superfície lateral deste recinto cilíndrico para sua superfície da base.
Um cone circular de diâmetro D é posicionado em um eixo comum com disco circular, também de diâmetro, D, a uma distância L, como mostrado na Fig. P13-18. Com uma área hipotética ( A 3 ) correspondente
130 - O número de fatores de forma que precisam ser avaliados diretamente para um recinto de 10 superfícies é(A) 1 (B) 10 (C) 22 (D) 34 (E) 45
126 - Considere duas esferas concêntricas com diâmetros de 12c m e 18c m formando um recinto cujas temperaturas de superfície são 300K . Assumindo que as superfícies são negras, a troca de radiação lí