Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 15

Como mostrado na figura, considere o disco A 1 localizado coaxialmente a 1   m de distância, porém inclinado 30 ° em relação à reta normal a uma coroa circular A 2 .

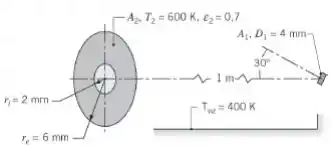
Qual é a irradiação sobre A 1 devido à radiação de A 2 , que é uma superfície cinza e difusa com emissividade de 0,7 ?

Passo 1

Nessa questão nós temos um disco A 1 , localizado coaxialmente, mas inclinado a 30 ° do normal, do disco A 2 em cinza difuso e em forma de anel com arredores a 400   K .

A partir disso, vamos encontrar a irradiação em A 1 , G 1 , devido à radiação de A 2 .

Passo 2

Para resolver essa questão vamos assumir que A 2 é superfície cinza difusa e que a radiosidade é uniforme sobre A 2 e que a área circundante é grande em relação a A 1 e A 2 .

A irradiação em A 1 é:

G 1 = q 21 A 1 = F 21 . J 2 A 2 A 1  

Onde J 2 é a radiosidade de A 2 avaliada como:

J 2 = ε 2 E b , 2 + ρ 2 G 2 = ε 2 σ T 2 4 + 1 - ε 2 σ T s u r 4

J 2 = 0,7 × 5,67 × 10 - 8 W m 2 . K 4 600 K 4 + ( 1 - 0,7 ) 5,67 × 10 - 8 W m 2 . K 4 400 K 4

J 2 = 5144 + 436 = 5580   W / m 2

Passo 3

Usando a relação de fator de forma da Eq. 13.8, avalie os fatores de vista entre A 1 ' , a projeção normal de A 1 e A 3 como,

F 1 ' 3 = D i 2 D i 2 + 4 L 2 = 0,004 m 2 0,004 m 2 + 4 1 m 2 = 4,00 × 10 - 6

E entre A 1 ' e ( A 2 + A 3 ) como:

F 1 ' ( 23 ) = D o 2 D o 2 + 4 L 2 = 0,0 12 m 2 0,0 12 m 2 + 4 1 m 2 = 3,6 0 × 10 - 5

Dando,

F 1 ' 2 = F 1 ' ( 23 ) - F 1 ' 3 = 3,60 × 10 - 5 - 4,00 × 10 - 6 = 3,20 × 10 - 5

Passo 4

Da relação de reciprocidade, conclui-se que:

F 21 ' = A 1 ' F 1 ' 2 A 2 = A 1 cos ⁡ θ 1 A 2 F 1 ' 2 = 3,20 × 10 - 5 cos ⁡ θ 1 A 1 A 2

Por inspeção, notamos que toda a radiação que atinge A 1 ' também interceptará A 1 , isso é:

F 21 = F 21 '  

Portanto,

G 1 = 3,20 × 10 - 5 cos ⁡ θ 1 A 1 A 2 × J 2 × A 2 A 1 = 3,20 × 10 - 5 cos ⁡ θ 1 × J 2

G 1 = 3,20 × 10 - 5 cos ⁡ ( 30 ° ) × 5580 W m 2 = 27,7   μ W / m 2

Resposta

G 1 = 27,7   μ W / m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o fator de forma das ranhuras muito longas mostradas na Fig. P13–17 para o lado externo, sem usar tabelas ou gráficos de fatores de forma. Despreze os efeitos das extremidades.
Determine o fator de forma F 12 entre as superfícies retangulares mostradas na Fig. P13–15.
Considere um recinto cônico de altura h e diâmetro da base D. Determine o fator de forma a partir da superfície lateral cônica para um furo de diâmetro d localizado no centro da base.
Dois cilindros paralelos infinitamente longos, de diâmetro D, estão localizados a uma distância s um do outro. Determine o fator de visão F 12 entre esses dois cilindros.
Repita o Problema 13-19 com L = D .