Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 16

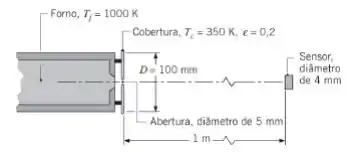
Um sensor de fluxo térmico com 4   m m de diâmetro está posicionado normal e a 1   m de distância da abertura, com 5   m m de diâmetro, de um forno a 1000   K que se comporta como um corpo negro. A cobertura que protege a abertura do forno, cinza e difusa ( ε   =   0,2 ) , tem um diâmetro externo de 100   m m e sua temperatura é de 350   K . O forno e o sensor estão localizados no interior de uma grande sala cujas paredes têm uma emissividade de 0,8 e estão a 300   K .

(a) Qual é a irradiação sobre o sensor, G s ( W / m 2 ) , considerando somente a emissão a partir da abertura do forno?

(b) Qual é a irradiação sobre o sensor devido à radiação a partir da cobertura e da abertura?

Passo 1

Nessa questão nós temos um medidor de fluxo de calor posicionado normal em um forno de corpo negro. E temos que a cobertura do forno é de 350   K , enquanto o ambiente é de 300   K .

A partir disso vamos encontrar a irradiação no medidor, G g , considerando apenas a emissão da abertura do forno e a irradiação considerando a radiação da tampa e da abertura.

Passo 2

Para resolver essa questão vamos assumir que:

(1) A abertura do forno aproxima-se do corpo negro;

(2) A blindagem é opaca, difusa e cinza com temperatura uniforme;

(3) A blindagem possui uma radiosidade uniforme;

(4) A g   < <   R 2 , de modo que ω g - f = A g R 2 ;

(5) Os arredores são grandes, uniformes a 300   K .

A irradiação no medidor devido apenas à emissão da abertura é:

G g = q f - g A g = I e , f . A f . cos ⁡ θ f . ω g - f A g = σ T f 4 π . A f . A g R 2   / A g

G g = σ T f 4 π R 2 . A f = 5 , 67 × 10 - 8 W m 2 . K 4   1000   K 4 π 1 m 2 × π 4 0,005 m 2 = 354,4   m W / m 2

Passo 3

A irradiação no medidor devido à radiação da abertura (a) e da tampa (c) é:

G g = G g , a + F c - g . J c A c A g

Onde F c - g e a radiosidade da capa são:

F c - g = F c - g A g A c ≈ D c 2 4 R 2 + D C 2 . A g A c

J c = ε c E b T c + ρ c G c

Passo 4

Mas,

G c = E b ( T s u r )

E,

ρ c = 1 - α c = 1 - ε c

J c = ε c σ T c 4 + ( 1 - ε c ) σ T s u r 4

J c = 170,2 + 387,4 W / m 2

Então, a irradiação é:

G g = G g , a + 1 A g D c 2 4 R 2 + D C 2 . A g A c ε c σ T c 4 + 1 - ε c σ T s u r 4 A c

Substituindo os valores,

G g = 354,4 m W m 2 + 0,10 2 4 × 1 2 + 0,10 2 0,2 × σ 350 4 + 1 - 0,2 × σ 3 0 0 4 W m 2

G g = 1695   m W / m 2

Resposta

  1. G g = 354,4   m W / m 2
  2. G g = 1695   m W / m 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o fator de forma, F 12 , para os retângulos mostrados nas figuras.
Uma pista de patinação no gelo circular com 25m de diâmetro encontra-se coberta por uma cúpula hemisférica com 35m de diâmetro. Se as superfícies do gelo e da cúpula puderem ser aproximadas por corpos
Um forno de secagem é constituído por um longo duto semicircular com diâmetro D=1m . Os materiais a serem secados cobrem a base do forno, enquanto a parede é mantida a 1200K . Qual é a taxa de secagem
Dois projetos de forno, como ilustrados e dimensionados no Problema 13.4, são usados para aquecer um corpo de prova em forma de disco ( A 1 ) . A potência fornecida aos fornos cônico e cilíndrico ( A
Um aquecedor tubular com a superfície interna negra de temperatura uniforme T s =1000K irradia um disco que se encontra em posição coaxial ao tubo.(a) Determine a potência radiante oriunda do aquecedo