Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 42

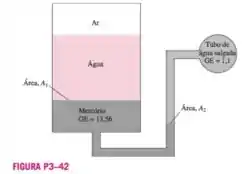
Considere o sistema mostrado na Figura P3 – 42. Se uma alteração de 0,7   k P a na pressão do ar fizer com que a interface entre a água salgada e o mercúrio da coluna da direita caia em 5   m m no nível da água salgada da coluna da direita, enquanto a pressão do tubo de água salgada permanece constante, determine a relação A 2 A 1 .

Passo 1

Temos que as gravidades específicas são de 13,56 para mercúrio e 1,1 para salmoura. Vamos trabalhar com a densidade padrão da água que é ρ w   =   1000 k g m 3 .

Note que na declaração do problema e na figura, que a pressão da salmoura é muito maior que a pressão do ar e, quando a pressão do ar cai 0,7 kPa, a diferença de pressão entre a salmoura e o espaço aéreo também aumenta na mesma quantidade.

Passo 2

Bom, iremos começar com a pressão do ar (ponto A) e movendo-se ao longo do tubo adicionando (à medida que descemos) ou subtraindo (à medida que subimos) os termos ρ g h até chegarmos ao tubo de salmoura (ponto B).

Definindo o resultado igual a P B antes e depois da mudança de pressão do ar, temos que:

Antes:

P A 1 + ρ w g h w + ρ H g g h H g , 1 - ρ s a l m o u r a g h s a l m o u r a , 1 = P B

Depois:

P A 2 + ρ w g h w + ρ H g g h H g , 2 - ρ s a l m o u r a g h s a l m o u r a , 2 = P B

Passo 3

Agora iremos subtrair as duas equações, ou seja...

P A 2 - P A 1 + ρ H g g ∆ h H g - ρ s a l m o u r a g ∆ h s a l m o u r a = 0

P A 1 - P A 2 ρ w g = G E H g ∆ h H g - G E s a l m o u r a ∆ h s a l m o u r a = 0

Onde Δ h H g e Δ h s a l m o u r a são as alterações nas alturas diferenciais da coluna de mercúrio e salmoura, respectivamente, devido à queda na pressão do ar.

Ambas são quantidades positivas, pois, à medida que a interface mercúrio-salmoura cai, as alturas diferenciais do fluido para mercúrio e salmoura aumentam.

Passo 4

Observando também que o volume de mercúrio é constante, temos...

A 1 ∆ h H g ,   e s q u e r d a = A 2 ∆ h H g ,   d i r e i t a

E logo, também...

P A 2 - P A 1 = - 0,7   k P a = - 700 N m 2 = - 700 k g m ∙ s 2

∆ h s a l m o u r a = 0,005   m

∆ h H g = ∆ h H g ,   d i r e i t a + ∆ h H g ,   e s q u e r d a = ∆ h s a l m o u r a + ∆ h s a l m o u r a A 2 A 1 = ∆ h s a l m o u r a 1 + A 2 A 1

Realizando a substituição:

700 k g m ∙ s 2 1000 k g m 3 9,81 m s 2 = [ 13,56 × 0,005 1 + A 2 A 1 - 1,1 × 0,005 ] m

E, portanto,...

A 2 A 1 = 0,134

Resposta

Por fim, teremos que a relação A 2 A 1 é...

A 2 A 1 = 0,134

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As seguintes medidas de pressão e temperatura foram tomadas por um balão meteorológico subindo através da atmosférica inferior:Os valores iniciais (no topo da tabela) correspondem ao nível do solo. Us
Uma porta de acesso, de 1m de largura e 1,5m de altura, está localizada em uma parede plana e vertical de um tanque de água. A porta é articulada ao longo da sua borda superior, que está 1m abaixo da
Um elevador hidráulico-pneumático consiste em um conjunto pistão-cilindro pra içar a cabine do elevador. Óleo hidráulico armazenado em um tanque acumulador pressurizado por ar, aciona o pistão por mei
A leitura do barômetro de um alpinista indica 930m b a r s no início de uma expedição de alpinismo a 780m b a r s no final. Desprezando o efeito da altitude sobre a aceleração da gravidade, determine
A leitura de um medidor de pressão conectado a um tanque é de 500k P a em um local onde a pressão atmosférica é de 94k P a . Determine a pressao absoluta no tanque.