Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 39

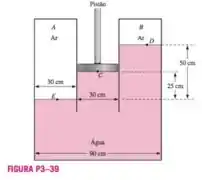
Duas câmaras com o mesmo fluido na base estão separadas por um pistão com peso 25 N, como mostra a Figura P3-39. Calcule as pressões manométricas das câmaras A e B.

Passo 1

Para esse exercício, note que o pistão está em equilíbrio e, portanto, a força resultante que atua no pistão deve ser zero.

Porém, temos que um equilíbrio de força vertical no pistão envolve a força da pressão exercida pela água na face do pistão, a força da pressão atmosférica e o peso do pistão, portanto temos que:

P C A p i s t ã o = P a t m A p i s t ã o + W p i s t ã o

P C = P a t m + W p i s t ã o A p i s t ã o

Passo 2

Muito bem!! Agora a pressão no fundo de cada câmara de ar é determinada a partir da relação da pressão hidrostática, ou seja, teremos a formulação abaixo:

P a r A = P E = P C + ρ g C E - = P a t m + W p i s t ã o A p i s t ã o + ρ g C E -

P a r A ,   m a n ô m e t r i c a = W p i s t ã o A p i s t ã o + ρ g C E -

E

P a r B = P D = P C + ρ g C D - = P a t m + W p i s t ã o A p i s t ã o + ρ g C D -

P a r B ,   m a n ô m e t r i c a = W p i s t ã o A p i s t ã o - ρ g C D -

Passo 3

Portanto, agora basta substituirmos os valores...

P a r A ,   m a n ô m e t r i c a = 25   N π 0,3   m 2 4 + 1000 k g m 3 9,81 m s 2 0,25   m 1   N 1 k g ∙ m s 2

P a r A ,   m a n ô m e t r i c a = 2806 N m 2 = 2,81 k P a

E

P a r B ,   m a n ô m e t r i c a = 25   N π 0,3   m 2 4 - 1000 k g m 3 9,81 m s 2 0,25   m 1   N 1 k g ∙ m s 2

P a r B ,   m a n ô m e t r i c a = - 2099 N m 2 = - 2,10 k P a

Resposta

Portanto as pressões manométricas das câmaras A e B respectivamente são:

P a r A ,   m a n ô m e t r i c a = 2,81 k P a

P a r B ,   m a n ô m e t r i c a = - 2,10 k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um medidor manométrico e um manorômetro são anexados a um tanque de gás para medir sua pressão. Se a leitura do medidor manométrico de pressão for 80k P a , determine a distância entre os dois níveis
Repita o Problema 3-24 para uma diferença de altura de mercúrio de 30m m .
Um manômetro a merairio ( ρ =13 . 600k g / m 3 ) está conectado a um duto do ar para medir a pressão interna. A diferença nos níveis do manômetro é de 15m m e a pressão atmosférica é de 100k P a . (a)
A pressão sanguínea em geral é medida colocando-se um involucro cheio de ar e fechado equipado com um medidor manométrico de pressão ao redor da parte superior do braço de uma pessoa no nível do coraç
A pressão sanguínea máxima na parte superior do braço de uma pessoa saudável é de cerca de 120m m H g . Se um tubo vertical aberto para a atmosfera estiver conectado à veia do braço da pessoa, determi