Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 72

Considere uma superfície difusa e opaca cuja refletividade espectral varia em função do comprimento de onda conforme ilustrado. A superfície se encontra a 750   K e a irradiação sobre um dos seus lados varia em função do comprimento de onda conforme ilustrado. O outro lado da superfície está isolado termicamente.

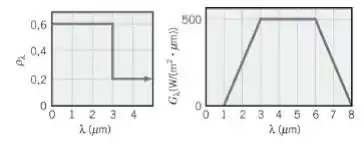
Quais são a absortividade e a emissividade totais da superfície? Qual é o fluxo térmico radiante líquido para a superfície?

Passo 1

Nessa questão nós temos uma superfície opaca e difusa com refletividade espectral dada e a uma temperatura de 750 K que é submetida a uma irradiação espectral fornecida, G λ .

Com isso , vamos encontrar a absortividade total,   α , a emissividade total, ε , e o fluxo de calor radiativo líquido para a superfície.

Passo 2

Para resolver essa questão vamos assumir que a superfície é opaca e difusa e a parte traseira é isolada. A absortividade total é determinada a partir de,

α λ = 1 -   ρ λ

E,

α = ∫ 0 ∞ α λ G λ d λ G  

Avaliando por integrais separadas em vários intervalos de comprimento de onda temos,

α = 1 - ρ λ , 1 ∫ 1 3 G λ d λ + 1 - ρ λ , 2 ∫ 3 6 G λ d λ + 1 - ρ λ , 2 ∫ 6 8 G λ d λ ∫ 1 3 G λ d λ + ∫ 3 6 G λ d λ + ∫ 6 8 G λ d λ = G a b s G

G = 0,5 × 500 W m 2 . μ m × 3 - 1 μ m + 500 W m 2 . μ m × 6 - 3 μ m + 0,5 × 500 W m 2 . μ m × 8 - 6 μ m

α = 200 + 1200 + 400 W / m 2 5 00 + 1 5 00 + 5 00 W / m 2 = 1800   W / m 2 25 00   W / m 2 = 0,720

Passo 3

A emissividade total da superfície é determinada por,

ε λ = α λ

E então,

ε λ = 1 - ρ λ

A emissividade total pode então ser expressa como,

ε = ∫ 0 ∞ ε λ E λ , b λ ,   T s E b ( T s ) d λ = ∫ 0 ∞ ( 1 - ρ λ ) E λ , b λ ,   T s E b ( T s ) d λ

ε = 1 - ρ λ , 1 ∫ 0 3 E λ , b λ ,   T s E b T s d λ + ( 1 - ρ λ , 2 ) ∫ 3 ∞ E λ , b λ ,   T s E b ( T s ) d λ

ε = 1 - ρ λ , 1 F 0 - 3 μ m + 1 - ρ λ , 2 1 - F 0 - 3 μ m

Usando a tabela 12.1 para λ 1   T s = 3 × 750 K = 2250 μ m . K ,   F ( 0 - λ ) = 0,111 ,

ε = ( 1 - 0,6 ) × 0 , 111 + ( 1 - 0,2 ) 1 - 0 , 11 1 = 0,7 56

Passo 4

O fluxo de calor radiativo líquido para a superfície é,

q r a d ' ' = α G - ε E b T s = α G - ε σ T s 4

Substituindo os valores,

q r a d ' ' = 0,720 × 2500 W m 2 - 0,756   5,67 ×   10 - 8 W m 2 . K 4 750   K 4

q r a d ' ' = - 11763   W / m 2

Resposta

α = 0,720

ε = 0,756

q r a d ' ' = - 11763   W / m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma superfície difusa, que apresenta as características espectrais a seguir, é mantida a 500K quando localizada no interior de um grande forno cujas paredes são mantidas a 1500K :(a) Esboce a distribu
Um vidro difuso especial, com propriedades radiantes espectrais conhecidas, é aquecido no interior de um grande forno. As paredes do forno, que são mantidas a T p = 1800K , são revestidas com um tijol
Duas superfícies pequenas, A e B, estão localizadas no interior de um recipiente isotérmico a uma temperatura uniforme. O recipiente proporciona uma irradiação de 6300W / m 2 em cada uma das superfíci
Uma placa horizontal opaca tem uma espessura de λ=21m m e condutividade térmica de k=25W / ( m·K ) . Água escoa em contato com a superfície inferior da placa e está a uma temperatura de T ∞ , a g =25